А) АВ1 принадлежит плоскости АА1В1В
Д1С принадлежит плоскости ДД1С1С
Эти плоскости параллельные, тк это грани куба, следовательно эни не пересекаются
Значит, прямые, лежащие в этих плоскостях будут скрещивающимися
Б) параллельно переносим Д1С в плоскость АА1В1В, чтобы совместить точки В1 и С
Тк эти прямые были диагоналями сторон куба, между ними будет угол 90 градусов
В) ВВ1 принадлежит плоскости АА1В1В, эта плоскость параллельна плоскости СС1Д1Д.
А все прямые лежащие в плоскости, которая параллельна этой плоскости тоже параллельны той плоскости
Пусть даны наклонные АВ и АС и перпендикуляр к плоскости АО. Если х - коэффициент пропорциональности, то АВ=5х, АС=6х. Проецией наклонной АВ является отрезок ВО=4 см, а проекцией наклонной АС является отрезок СО=3корня из3. Найдем АО из треугольника АВО по теореме Пифагора: АО^2=AB^2-BO^2=25x^2-16; найдем АО из треугольника АСО по теореме ПИфагора: АО^2=АС^2-CO^2=36x^2-27.Приравняем правые части получившихся выражений 25х^2-16=36x^2-27
11x^2=11
x=1 - коэффициент пропорциональности, то АВ=5 см и АО=3 см
ответ: 3 см
(см. объяснение)
Объяснение:
Перед нами уравнение квадрата, точка пересечения диагоналей которого имеет координаты (0; 0) и расстояние от точки пересечения диагоналей которого до одной из вершин равно 4.
Зная это, построим график:
(см. прикрепленный файл)
Задание выполнено!
Комментарий 1:
Функция непрерывна и при любом раскрытии модуля будет получаться уравнение прямой: либо y=-x+4, либо y=-x-4, либо y=x-4, либо y=x+4. Строим их до пересечения, таким образом получая график.
Комментарий 2:
Функция непрерывна и при любом раскрытии модуля будет получаться уравнение прямой, причем точки "склеивания" будут в координатах (0; 4), (4; 0), (-4; 0), (0; -4). Тогда соединим их и получим график.
Комментарий 3:
При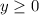
получим график модуля 
.
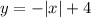При
будет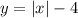 
.
Строим это и получаем график.