Точка А находится на расстоянии 4 см от центра окружности и делит хорду ВС длиной 9 см на отрезки, разность которых равна 1 см. Найдите радиус окружности. ответ.
Номер 1. Т.к треугольник прямоугольный, то один из углов 90градусов по опр. Значит т.к треугольник еще и р/б, то по свойству у него два угла при основании равны. Если среди них есть угол в 90градусов то их сумма 180градусов, что противоречит теорема о сумме углов в треугольника, значит эти углы по (180-90)/2=45градусов. ответ:90,45,45 Номер 2. Т.к треугольник CDE - р/б, то угол C равен углу E, значит т.к угол D равен 54градуса, то угол E=(180-54)/2=63градуса. То т.к CF - высота, то угол CFE=90градусов, следовательно угол ECF=180-54-63=63градуса ответ:63градуса Надеюсь все понятно объяснил.
1. В тексте исправил вопрос на "найти длину проекции наклонной", а то получается , что искать нужно известную величину. Угол между наклонной и плоскостью - это угол между наклонной и ее проекцией на плоскость. Имеем прямоугольный треугольник: гипотенуза 8 см, один угол 60°. ВТОРОЙ ОСТРЫЙ 30°. Катет, лежащий против него равен половине гипотенузы, 8/2 = 4 см.Это проекция наклонной. Расстояние (это длина перпендикуляра) равно 4 * sin 60° = 2√3 см. 2. строим линейный угол двугранного угла и ставим размеры. Получаем прямоугольный треугольник с катетом 4 м и гипотенузой 8 м. Значит, угол равен 30°.
Відповідь:
Пояснення:
пусть один отрезок равен х, тогда другой равен х-1
х + х - 1 = 9, тогда 2х= 10 и отсюда х = 5 см = и х-1 = 4 см
также проведём ОВ (на рисунке нет). За теоремой Пифагора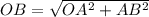
тогда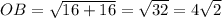
= R(на рисунке я провёл OR, но тупанул, ведь OB это уже радиус)