Понятно, зачем нам сказано, что биссектрисы пересекаются в одной точке - ведь эта точка равноудалена от . сторон четырехугольника и поэтому является центром вписанной окружности. А раз в четырехугольник можно вписать окружность, суммы противоположных сторон равны. Таким образом, ME+BD=MD+BE. Это равенство позволяет найти третью сторону треугольника, используя связь между сторонами и медианами треугольника, а также тот факт, что медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Пусть AB=c, BC=a, CA=b, тогда
. Поэтому
а умножив для упрощения это равенство на 6 и подставив b=12 и c=10, получаем
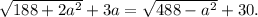
При всей моей любви к иррациональным уравнениям, решать это уравнение не хочется. Давайте попробуем угадать решение. И если Вы достаточно настойчивы, то удача в этой задаче к Вам придет - подходит a=10. (
). Другого решения быть не может, поскольку при a>0 правая часть возрастает, а левая убывает.
Таким образом, мы доказали, что наш треугольник равнобедренный со сторонами 12, 10 и 10. Иными словами, он состоит из двух прямоугольных треугольников с гипотенузой 10 и катетом 6, то есть треугольников, подобных египетскому 3-4-5. Площадь египетского треугольника равна 6, подобного треугольника с коэффициентом подобия 2 равна 24, а поскольку их два, суммарная площадь равна 48.
И наконец, кто не знает формулу для длины медианы, можно воспользоваться или теоремой косинусов, или теоремой Стюарта, или теоремой о сумме длин диагоналей параллелограмма.
верхнего ВСВ1 и
нижнего АДА1,- и
площади боковой поверхности цилиндра АВВ1А1.
Формула площади боковой поверхности конуса через радиус (R) и образующую (L):
Sбок. кон.=πRL
Радиус конуса здесь равен высоте ромба.
Так как диагонали АС и ВД ромба пересекаются под прямым углом и точкой пересечения делятся пополам,
высоту ромба можно найти из прямоугольного треугольника СОД - точнее, половину высоты ромба.
Треугольник СОД- "египетский", поэтому
СД=5 (проверьте по т. Пифагора)
Высота в прямоугольном треугольнике равна произведению катетов, деленному на гипотенузу ( из формулы площади прямоугольного треугольника)
ОН=ОС*ОД:СД=4*3:5=2,4 см
Высота МН ромба вдвое длиннее и равна 4,8 см
Sбок. кон.=πRL
Sбок. кон=4,8*5π=24π см²
2 Sбок. кон= 2*24π=48π ( площадь боковая конусов ВСВ1+АДА1)
Формула площади боковой поверхности цилиндра:
Sбок. цил=2πRh, и высота h здесь равна стороне ромба АВ =5 см
Sбок. цил=2π4,8*5=48π см ²
Полная площадь фигуры, образованной вращением ромба вокруг его стороны, равна
Sполн.= 48π+48π=96π см²