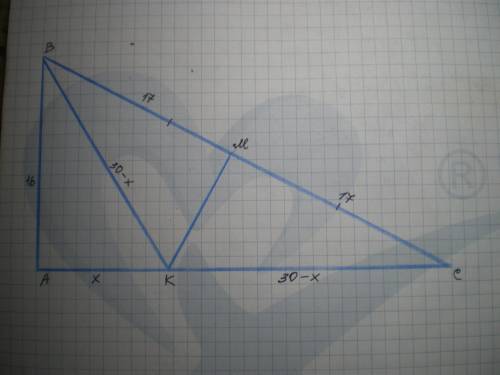
Дано: ΔАВС - прямокутний, ∠А=90°, АС=30 см, ВС=34 см; МК⊥ВС, ВМ=МС. Знайти МК.
Знайдемо АВ за теоремою Піфагора:
АВ=√(ВС²-АС²)=√(1156-900)=√256=16 см.
Проведемо ВК і розглянемо ΔВКС - рівнобедрений, тому що ВМ=СМ і МК⊥ВС, отже ВК=КС.
Нехай АК=х см, тоді КС=ВК=30-х см.
Знайдемо АК з ΔАВК - прямокутного:
АВ²=ВК²-АК²; 16² = (30-х)² - х²; 256=900-60х+х²-х²;
60х=900-256=644; х=10 11/15 см. АК=10 11/15 см, тоді
ВК = 30 - 10 11/15 = 19 4/15 = 289/15 см.
Знайдемо МК за теоремою Піфагора з ΔВМК, де ВМ=34:2=17 см.
МК²=ВК²-ВМ²=(289/15)² - 17² = (83521/225) - 289 = 18496/225.
МК=√(18496/225)=136/15=9 1\15 см.
Відповідь: 9 1/15 см.
№33на наклонная составляет с плоскостью угол 45 градусов.№32Точка А отстоит от плоскости на расстоянии 26 см. Найдите длину №31Дан куб ABCDA1B1C1D1,1) Выпишите грани, параллельные ребру AA12) выпишите рёбра, скрещивающиеся с ребром ВС3) выпишите рёбра, перпендикулярные плоскости (ABB1) 4) выпишите плоскости, перпендикулярные ребру AD.№30Радиусы оснований усечённого конуса равны Здм и 7дм. Образующая - 5дм. Найдите площадь осевого сечения.№29Шар пересечён плоскостью на расстоянии Зсм от центра. Найдитеплощадь сечения, если радиус шара равен 5см.№28Измерения прямоугольного параллелепипеда равны 8см, 12см, 18см.
Пусть B-Начало координат
Ось X - BC
Ось Y - перпендикулярно X в сторону A
Ось Z - MB
Найдем MB из треугольника MAB = √(6^2-3^2)= 3√3
Координаты точек
E (1/2;√3/2;0)
D (2,5;√3/2;0)
L( 1;√3;√3)
Уравнение плоскости основания ABC
z=0
Уравнение плоскости EDL
ax+by+cz+d=0
Подставляем координаты точек E D L
a/2+√3b/2+d=0
2,5a+√3b/2 + d =0
a+√3b+√3c + d=0
a=0 Пусть d = - √3/2 тогда b=1 c= -1/2
Уравнение EDL
y - z/2 -√3/2=0
Косинус искомого угла равен
| (0;0;1) * (0;1;-1/2) | / | (0;0;1) | / | (0;1;-1/2) | = 1/√5
Cам угол - arccos(√5/5)