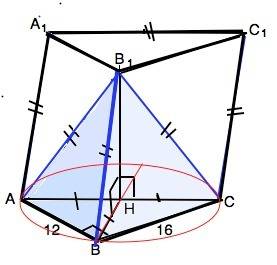
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
ответ: например
Объяснение:Cos (a+b)=cos(a-(-b))=cos a*cos(-b)+sin a*sin (-b)= cos a*cos b-sin a*sin b значит cos(a+b)=cos a*cos b- sin a*sin b. Докажем формулу (4): sin. (a+b)=cos(пи/2-(a+b))=cos((пи/2-a)-b)=cos(пи/2-a)cos b+sin(пи/2-a)sin b=sin a*cos b+cos a*sin b Значит sin (a+b)=sin a*cos b+sin b*cos a Докажем формулу (3) Применяя последнюю формулу имеем sin(. ... ф-ция y=cos x-четная. Из формул сложения пологая b=пи n/2, где n ÎN, можно вывести формулы привидения для преобразований выражений вида cos(пи*n/2 ±a), sin(пи*n/2 ±a). Например cos(пи*n/2 -a)= cos пи/2*cos a+sin пи/2*sin a=0+sin a=sin a. Аналогично выводятся следующие формулы: Sin.
№1.
1) R = 7 см > S = 4πR² = 4π*7² = 4π*49 = 196π (см²);
2) R = 3 дм > S = 4πR² = 4π*3² = 4π*9 = 36π (дм²).
№2.
1) R = 2 дм > S = 4πR² = 4π*2² = 4π*4 = 16π (дм²);
2) R = 4 см > S = 4πR² = 4π*4² = 4π*16 = 64π (см²).
№3.
Dс = 400 Dл
Sп.С/Sп.л. --- ?
Dс = 400 Dл
2Rс = 400 * 2Rл
Rс = 400 Rл
Sп.С/Sп.л. = 4πRс²/4πRл² = Rс²/Rл² = (400 Rл)²/Rл² = 400² = 160000.