
По условию составим систему уравнений и решим ее.
b + a = 15
b - a = 9
сложим уравнения: 2b = 24; b = 12; ⇒ a = 3. Основания трапеции 12 и 3.
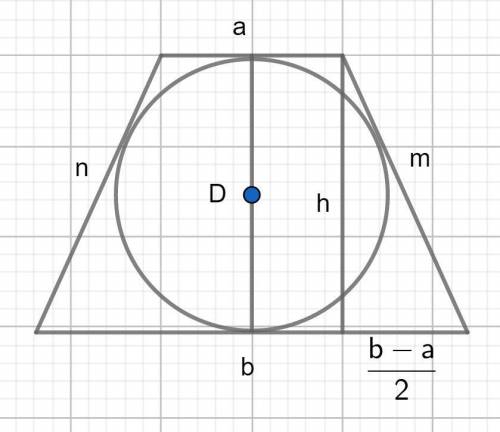
В трапецию вписана окружность, значит суммы противоположных сторон равны. a + b = m + n = 15.
Трапеция равнобедренная. ⇒ m = n = 15/2 = 7,5
Диаметр вписанной окружности равен высоте трапеции D = h.
В прямоугольном треугольнике гипотенуза = m = 7,5; меньший катет = (b-a)/2 = 4,5; больший катет равен высоте трапеции и диаметру вписанной окружности.
По т. Пифагора: D = h = √(7,5² - 4,5²) = 6
Диаметр вписанной окружности = 6.
Смари:
Нам дан прямоугольник, а как нам известно, в прямоугольнике у нас все углы равны 90°. Потом мы проводим диагональ от угла А до угла С, а там нам уже говорят, что угол, образованный благодаря этой диагонали (САД), равен 30°.
Что же мы теперь имеем? Прямоугольный треугольник с углами А, С и Д. Мы ведь уже знаем, что угол Д =90°(ну там выше написано), а угол САД =30°, а по какой-то там теореме или ещё чему-то мы знаем, что катет(такая маленькая сторона треугольника) равен половине гипотенузы (такая самая большая сторона в треугольнике), если он лежит на против угла в 30°. А т.к. нам ещё сказали, что диагональ(та же наша гипотенуза) равна 16см, то получается, что самый маленький катет равен 16:2=8 см. "А что же дальше?" спросишь ты... Наш катет является шириной нашего прямоугольника! Короче, там по условию длина на три см больше, чем ширина, так что просто 8+3=11см.
И мы узнали, что ширина равна 8см, а длина равна 11.
Еее
Р=48см
Объяснение:
В равнобедренном треугольнике биссектриса является ещё высотой и медианой, поэтому она делит сторону АС пополам, и так как ∆АВС равнобедренный, то периметры ∆АВМ и ∆СВМ равны. Сумма сторон
АВ+АМ=ВС+СМ=34–10=24см.
Тогда периметр ∆АВС=24×2=48см