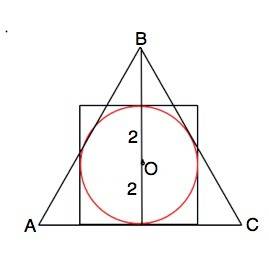
1. Правильный четырехугольник - квадрат.
Диаметр вписанной в квадрат окружности равен стороне квадрата. ⇒ r=d:2=4:2=2 см.
Для описанного вокруг данной окружности треугольника АВС она - вписанная.
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты. Следовательно, высота ∆ АВС =2•3=6 см.
Тогда АВ=ВН:sin60°=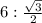
=4√3 см.
* * *
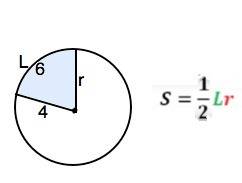
2. Для нахождения площади сектора существует формула.
S=Lr:2, где L – длина дуги сектора. ⇒
S=6•4:2=12 см²
Если формула забыта, решить задачу можно без нее.
Длина окружности C=2πr
C=2•p•4=8π см
Площадь окружности S=πr²=16 π см²
Вычислим площадь, которая приходится на сектор с дугой в 1 см.
S:C=16π:8π=2
Тогда площадь сектора
S=2•6=12 см²
1)нет
2)да
3)нет
4)бессектриса
5)равнобедренный
6)хз
7)Окружность называется вписанной в треугольник, если она касается через все его сторон.
Теорема.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Доказательство.
Пусть ABC данный, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами. Δ AEO = Δ AOD по гипотенузе и катету (EO = OD – как радиус, AO – общая). Из равенства треугольников следует, что ∠ OAD = ∠ OAE. Значит AO биссектриса угла EAD. Точно также доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.
7) хз
