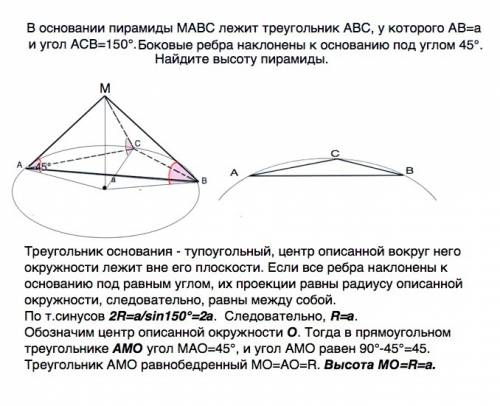
Треугольник основания - тупоугольный, ⇒ центр описанной вокруг него окружности лежит вне его плоскости.
Если все ребра пирамиды наклонены к основанию под равным углом, их проекции равны радиусу описанной окружности, следовательно, равны между собой.
По т.синусов 2R=a/sin150°=2а. ⇒ R=а.
Обозначим центр описанной окружности О.
Тогда в прямоугольном ∆ АМО ∠МАО=45°, и ∠АМО равен 90°-45°=45°. ∆ АМО равнобедренный ⇒МО=АО=R. Высота МО=R=a.
---------
Рисунок для наглядности дан не совсем соразмерным условию.
L=2pr или L=pD ,где D=2r
1) L=6*2*3.14=37.68см
2) L=1.4*2*3.4=8.792м