Впрямоугольнике авсд биссектриса угла а пересекает сторону вс в точке о, доказать, что треугольник аво - id413423620210713 от smorodina83 13.07.2021 12:08

Question

Геометрия: Впрямоугольнике авсд биссектриса угла а пересекает сторону вс в точке о, доказать, что треугольник аво - равнобедренный. решить

smorodina83 · Accepted Answer

Выведу обобщённую формулу для подобных задач про трапецию с известными диагоналями AC = x, BD = y, и суммой оснований BC + AD = m

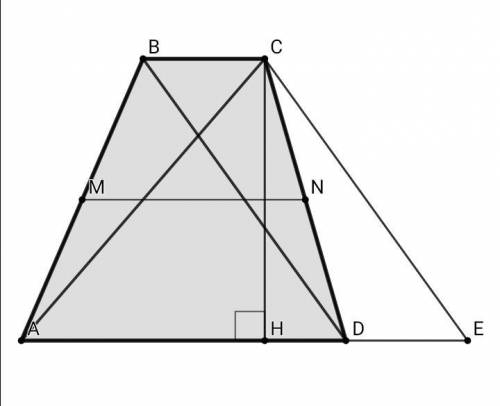
Проведём из вершинны С прямую СЕ, параллельную BD, тогда BC || DE, CE || BD ⇒ BCED - параллелограми, ВС = DE, CE = BD = y

S (abcd) = (BC + AD)•CH/2 = (DE + AD)•CH/2 = AE•CH/2 = S (ace)

Площадь трапеции ABCD равна площади треугольника ACE

Найдём плошадь ΔАСЕ по формуле Герона: АС = х, CE = y, AE = m

Площадь трапеции с диагоналями х и у и суммой оснований равной m:S = √( p • (p - x) • (p - y) • (p - m) ) , где р = (х + y + m)/2

Средняя линия трапеции: MN = (BC + AD)/2 = 5 ⇒ m = 10, x = 9, у = 17

S (abcd) = √(18•(18 - 9)(18 - 17)(18 - 10)) = √(18•9•1•8) = 36

ответ: 36

Впрямоугольнике авсд биссектриса угла а пересекает сторону вс в точке о, доказать, что треугольник аво - равнобедренный. решить