Рассмотрим равнобедренный треугольник ABC с боковыми сторонами AB = BC и основанием AC.
Опустим из вершины B высоту BH на основание AC.
Рассмотрим треугольники ABH и BCH.
Так как BH - высота, то углы BHA = BHC = 90°, т.е. треугольники ABH и BCH - прямоугольные.
Заметим, что AB = BC, т.е. гипотенузы треугольников ABH и BCH равны и у них общий катет BH.
Следовательно, треугольники ABH и BCH конгруэнтны по гипотенузе и катету.
Отсюда вытекает, что AH = CH, а это означает, что BH является медианой.
Также из равенства треугольников ABH и BCH имеем, что углы ABH = CBH.
Следовательно, BH является биссектрисой угла ABC.
3 cm²
Объяснение:
За теоремою Піфагора знайдемо другий катет
b²=c²-a²
b²=13-4
b²=9
b=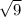
b=3
S=(a*b)/2
S=(2*3)/2
S=6/2=3