Так как отрезки РР₁ и ММ₁ перпендикулярны плоскости а, то указанные отрезки лежат на одной плоскости, а точка Р₁ лежит на отрезке КМ₁.
Рассмотрим ∆КРР₁ и ∆КММ₁.
Угол МКМ₁ – общий;
Угол КР₁Р=угол КМ₁М (оба прямые, так как РР₁ и ММ₁ перпендикулярны КМ₁)
Следовательно ∆КРР₁~∆КММ₁ по двум углам.
Пусть КР=n, тогда РМ=2n (из отношения КР:РМ=1:2), следовательно КМ=KP+PM=n+2n=3n.
Отношение двух любых сторон одного треугольника, равно отношению двух соответствующих сторон треугольника, подобного первому. Тогда:
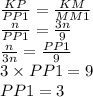
ответ: 3 см
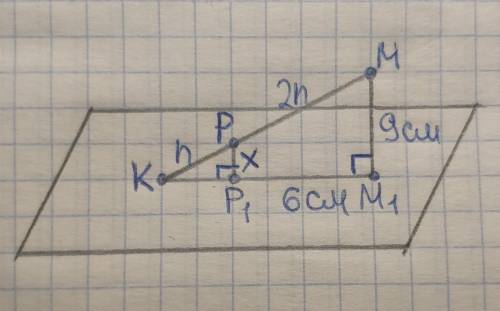
Сумма 4-х углов четырехугольника равна 360. Поскольку в паралелограмме противоположные углы равны, значит сумма двух соседних углов равна 180. Отнимаем 46 и делим на 2, получаем один угол 67, второй (+46) равен 113.
можно так:
Такие углы не могут быть противолежащими, так как они не равны. Значит, они прилежащие и их сумма равна 180°. Пусть один из углов равен х, тогда другой равен х+46°, по условию. Следовательно х+(х+46)=180
2х+46=180
2х=180-46
2х=134
х=67-первый,а второй х+46°=67+46=113 градусов
тогда что бы получился треугольник нужно что бы точка К по оси ординат отличалась от 0, то есть
Если О это начало координат то, координата
тогда площадь треугольника
Найдем угол между сторонами ОК и ОМ , по скалярному произведению рассмотрим как векторы