Можно найти площадь методом нахождения площади всех фигур, при этом прибавив их
Площадь прямоугольника с сторонами 5 и 1 = 5 ед.²
Опустим высоту с стороны прямоугольника длиной 1 ед. Она будет равняться 2, так как высота будет параллельна с высотой слева. У нас получился ещё один прямоугольник с сторонами 5 и 2. Его площадь равна 10 ед.² (если что, для площади прямоугольника мы умножаем стороны)
У нас также появился треугольник с сторонами 2 и (9-5) = 4. Найдём площадь данного треугольника: 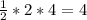 ед.²
ед.²
Треугольник слева будет равен треугольнику, который мы создали, так что его площади тоже равна 4 ед.²
Прибавляем все значения. Это равняется 23 ед.²
1.
АД=ДС(по условию), ВД - общая сторона.
т.к. угол ВДС=90°, то угол ВДА=180-90=90°(угол СДА - развернутый, значит он 180°)
Треугольники равны по двум сторонам и углу между ними (признак равенства треугольников)
2.
АО=ОВ (по условию)
уголСАО=уголОВС (по условию)
угол АОС=уголВОД (т.к. эти углы вертикальные, а вертикальные угды равны)
Треугольники равны по стороне и двум прилежащим к ней углам (признак равенства треугольников)
3.
АВ=ВС (по условию)
АД=ДС (по условию)
сторона ВД - общая
Треугольники равны по трем сторонам (признак равенства треугольников)