Противоположные углы параллелограмма равны. Углы, примыкающие к одной стороне - внутренние при пересечении параллельных прямых и секущей, их сумма равна 180°. ⇒
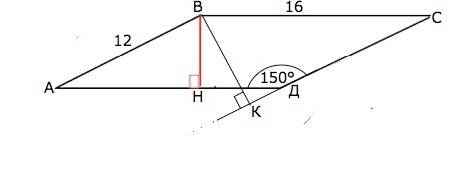
Угол ВАД=ВСД=180°-150°=30°.
Площадь параллелограмма равна произведению высоты на сторону, к которой проведена.
Высота ВН перпендикулярна стороне АД, ⇒∆ АВН - прямоугольный.
ВН противолежит углу 30° и равна половине гипотенузы АВ.
ВН=12:2=6 см.
S АВСД=ВН•АД=6•16=96 см²
Точно так же высота ВК, проведенная к СД, равна половине ВС, т.е. 8 см.
S АВСД=8•12=96 см²
Если одна из параллельных прямых пересекает плоскость, то другая прямая также пересекает эту плоскость.
Прямая АВ пересекает плоскость а. Тогда параллельная ей прямая СD (противоположные стороны параллелограмма попарно параллельны) также пересекает плоскость а. Аналогично, из того, что прямая ВС пересекает плоскость а, следует, что параллельная ей прямая AD также пересекает плоскость а.
Объяснение: