Відповідь:
Пояснення: На всех рисунках изображены пары подобных треугольников. По свойству сторон подобных треугольников (соответствующие стороны подобных треугольников пропорциональны) имеем:
k - коэффициентом подобия
А) Для данной пары треугольников коэффициент подобия равен: МК : АС = 16 : 4 = 4. Тогда: х • 4 = 12
х = 12 : 4 = 3
у = 6•4 = 24
Б) Для данной пары треугольников коэффициент подобия равен: АС : МК = 15 : 10 = 1,5. Тогда: х • 1,5 = х + 3
х • 1,5 - х = 3
0,5 • х = 3
х = 6
В) Для данной пары треугольников коэффициент подобия равен: ВД : АС = 10 : 5 = 2. Тогда: х = 6•2 = 12
у • 2 = 8
у = 4
32 cм²
Объяснение:
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:
Sбок= 1/2*(Р1+Р2)*L,
где Р1 и Р2 - периметры оснований пирамиды, L - апофема (высота боковой грани правильной усеченной пирамиды)
Найдём стороны оснований правильной четырехугольной усеченной пирамиды.
Диагональ квадрата: d = a√2, где а - сторона квадрата.
⇒ а = d/√2
АД = 6/√2 = 3√2, А1Д1= 2/√2 = √2.
Р1=4*АД= 4 * 3√2 = 12√2 см - периметр верхнего основания.
Р2=4*А1Д1=4√2 см - периметр нижнего основания пирамиды.
Найдем апофему L
Основания усеченной пирамиды - квадраты. Проведем из центров оснований перпендикуляры ОМ⊥ДС и О1М1⊥Д1С1. ОМ и О1М1 - радиусы вписанных окружностей в основания.
Т.к. r=a /2 (половина стороны основания), то
О1М1= А1Д1/2 =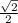
ОМ = АД/2 =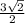
Опустим перпендикуляр М1К из точки М1 верхнего основания на нижнее основание. Получим прямоугольный ΔМ1КМ.
Т.к. М1К⊥КМ, КМ⊥ДС, то М1М⊥ДС ( по теореме о трёх перпендикулярах) ⇒∠М1МК = 60° (это данный нам линейный угол двугранного угла при ребре большего основания).
КМ = разнице расстояний от центров оснований до боковых сторон, то есть КМ = ОМ-О1М1=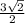
- 
= 
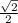см.
Тогда гипотенуза (апофема) L = ММ1 = КМ / cos 60° =
: 
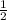= 2
cм
Sбок =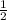
* ( 12
+ 4
) * 2
= 
(12+4) 
= 2*16=32 cм²