Р(квад) = 40 см
Р(прям) = 50 см
Р(квад) < Р(прям)
Объяснение:
Дано:
квадрат, со стороной 10 см
прямоугольник, одна из сторон 20 см
Sкв = Sпрям.
Найти:
Р(квад) - ?
Р(прям) - ?
Сравнить Р(квад) и Р(прям)
-----------------------
Даний:
квадрат, зі стороною 10 см
прямокутник, одна зі сторін 20 см
Ѕкв = Ѕпрям.
Знайти:
Р (квад) - ?
Р (прям) - ?
Порівняти р (квад) і Р (прям)
----------------------------
Решение
Пусть, S1 - площадь квадрата
S2 - площадь прямоугольника
a - сторона квадрата
m, n стороны прямоугольника
m = 20
----------------------------
Рішення
Нехай, S1-площа квадрата
S2-площа прямокутника
a-сторона квадрата
m, n - сторони прямокутника
m = 20
----------------------------
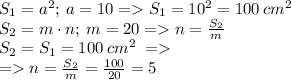
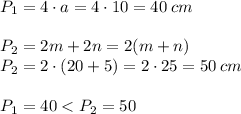
Следовательно, периметр прямоугольника больше периметра квадрата с той же площадью.
----------------------------
Отже, периметр прямокутника більше периметра квадрата з тією ж площею.
24 м² и 30°.
Объяснение:
Дано:
АВСА1В1С1-правильная усеченная пирамида
АВ=ВС=АС=8 см
А1В1=В1С1=А1С1=5 см
OO1= 3 см
Найти: площадь сечения и угол между ним и нижним основанием
1) СА1В - искомое сечение, т.к. точки А1С и А1В находятся в одних плоскостях.
2)Ось правильной усеченной пирамиды совпадает с осью соответствующей полной пирамиды, поэтому OO1 является высотой усеченной пирамиды. О1 — центр окружности, описанной около треугольника А1В1С1, О - центр окружности, вписанной в треугольник АВС.
Формула для радиуса описанной окружности около равностороннего треугольника:
R=а*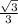
Формула для радиуса вписанной окружности в равносторонний треугольник:
r= а*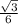
R=А1О1=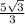
r=ОН=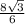 =
=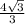
Проведем АН⊥ВС в ΔАВС. ОО1⊥(АВС)⇒ОО1⊥АН.
По теореме о трех перпендикулярах А1Н⊥ВС в ΔСА1В.
Угол ∠А1НА - линейный угол искомого двугранного угла.
Рассмотрим ΔА1О1К и ΔНОК.
∠А1О1К=∠НОК=90°, ∠А1КО1=∠НКО как вертикальные.
⇒ ΔА1О1К подобен ΔНОК ( по двум углам).
Из подобия Δ следует:
А1О1:ОН=О1К:КО
А1О1*КО=ОН*О1К
Пусть О1К= х, тогда КО=(3-х):
5√3(3-х)=4√3*х
9√3х=15√3
х=5/3
О1К = 5/3,
КО=3-5/3=4/3
ΔА1О1К(∠О1=90°): по т.Пифагора
А1К=√(А1О1²+О1К²)= √(75/9+25/9)=√(100/9)=10/3
ΔОКН(∠О=90°): по т.Пифагора
КН=√(ОН²+КО²)=√(16/9+48/9)=8/3
А1Н=А1К+КН=10/3+8/3=18/3=6 см
Площадь искомого сечения это площадь ΔСА1В:
S = 1/2 * ВС* А1Н = 1/2 * 8 * 6 = 24 см²
3) Рассмотрим ΔКОН(∠О=90°)
tg ∠KHO = KO/OH =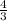 :
: 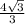 =
= 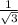
Тогда ∠KHO = 30°.
Т.к. ∠А1НА = ∠KHO, то ∠А1НА=30°