Объяснение:
Построим равнобедренную трапецию ABCD. Из вершины угла B проведем высоту(высота - это перпендикуляр, опущенный из вершины какого-либо угла к какой-то стороне). При проведении высоты образовался прямоугольный треугольник ABE, у которого угол A равен 30°. Вспомним геометрию 7-го класса: катет, лежащий напротив угла в 30°, равен половине гипотенузе. Так как у нас гипотенуза прямоугольного треугольника - это боковая сторона трапеции AB, а AB у нас равняется 10. Следовательно, катет BE будет равен 10 : 2 = 5 см.
Задача решена.
Будем считать, что задание дано так:
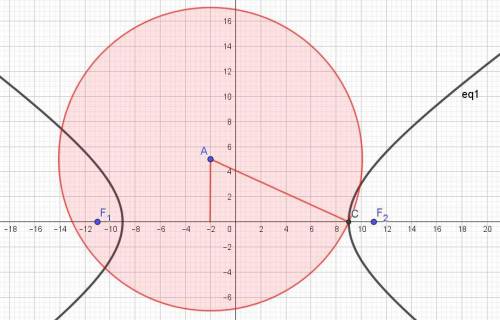
Определить уравнение окружности, проходящей через правую вершину гиперболы 40x² - 81y² = 3240 и имеющей центр в точке А(-2; 5).
Уравнение гиперболы приведём к каноническому виду, разделив обе части заданного уравнения на 3240:
(x²/81) - (y²/40) = 1.
Или так: (x²/9²) - (y²/(2√10)²) = 1 это и есть каноническое уравнение.
Отсюда находим координаты правой вершины гиперболы: С(9; 0).
Теперь находим радиус заданной окружности как отрезок АС.
АС = √((9 - (-2))² + (0 - 5)²) = √(121 + 25) = √146.
Получаем ответ: (x + 2)² + (y - 5)² = 146.
что это за язык чел не понимаю
Объяснение: