30
Объяснение:
треугольник АСР - прямоугольный ( угол С = 90 градусов)
сума углов треугольника 180 градусов, поэтому угол А = 180-(90+60) = 30 градусов
а далее свойство: катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы
ответ:Дан ромб АВСД. диагональ АС пересекает ВД в т.О
АС-меньная диагональ.УголВ=углу Д=60градусов.
Диагонали ромба делят углы пополам=> уголАДО=60:2=30градусов
диагонали ромба перпендикулярны => треугольник АОД прямоугольный.
Катет, лежащий напротив угла 30 градусов равен половине гипотенузы => АО=49:2=24,5
Диагонали ромба точкой пересечения делятся пополам => АС=2*АО=2/24,5=49
Можно и другим
Треугольник АСД - равносторонний, т.к. он равнобедренный (АД=ДС по св-вам ромба), углы при основании равны, а третий угол =60градусов => углы при основании тоже по 60 градусов => АД=АС=49
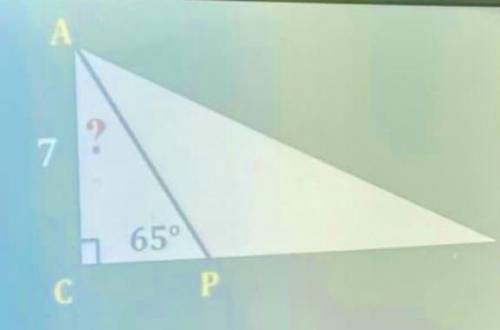
Объяснение:
По рисунку видим, что в ΔAPC:
∠C=90°
∠P=65°
∠A предстоит найти
Сумма углов любого треугольника равна 180°
То есть
∠A+∠C+∠P=180°
Тогда
∠A=180°-∠C-∠P=180°-90°-65°=25°
ответ: ∠A=25°