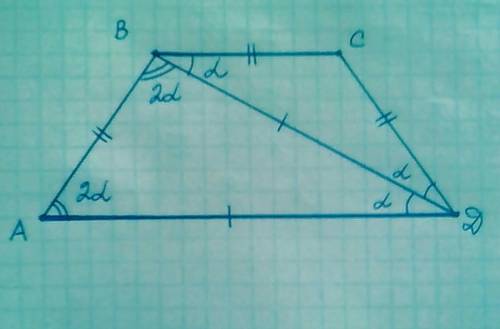
1) Рассмотрим ∆ ВСD:
Пусть угол CBD = a , тогда угол BDC = a, так как ∆ ВСD - равнобедренный
угол СBD = угол АDB = a - как накрест лежащие углы при ВС || АD и секущей BD
По свойству равнобедренной трапеции:
Углы при основании равнобедренной трапеции равны
Значит, угол BAD = угол ADC = 2a
2) Рассмотрим ∆ ABD:
∆ ABD - равнобедренный , поэтому угол BAD = угол АВD = 2a
Сумма всех углов в любом треугольнике всегда равна 180° =>
угол ВАD + угол ABD + угол ADB = 180°
2a + 2a + a = 180°
5a = 180°
a = 180° : 5 = 36°
Угол при меньшем основании ( ВС ) равнобедренной трапеции равен:
угол ABC = 3a = 3 × 36 = 108°
ОТВЕТ: 108°
1.
М - середина АВ, значит МВ = АВ/2
Р - середина МВ, значит РВ = МВ/2 = АВ/4
К - середина ВС, значит КС = ВС/2
Е - середина КС, значит ЕС = КС/2 = ВС/4
N - середина АС, значит NA = АС/2
G - середина NA, значит GA = NA/2 = AC/4
По условию
PB + EC + GA = 12
АВ/4 + ВС/4 + АС/4 = 12
1/4 · (АВ + ВС + АС) = 12
АВ + ВС + АС = 12 · 4 = 48 (см)
2.
Из решения первой задачи следует, что
АР = 3/4 АВ
ВЕ = 3/4 ВС
CG = 3/4 AC
По условию
AP + BE + CG = 108
3/4 АВ + 3/4 ВС + 3/4 АС = 108
3/4 · (АВ + ВС + АС) = 108
АВ + ВС + АС = 108 · 4/3 = 144 (см)