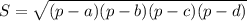Площадь боковой поверхности состоит из 6-ти одинаковых равнобедренных треугольников со сторонами 13 и основанием 10 (так как шестиугольная пирамида правильная). Найдем площадь одной грани такой пирамиды. Будем ее искать по формуле
,
где a=10 – основание треугольника; h – высота треугольника. Так как треугольник равнобедренный, то его высота, проведенная к основанию a будет делить это основание пополам. Следовательно, высоту можно найти из прямоугольного треугольника с катетом 5 и гипотенузой 13 по теореме Пифагора:
и площадь одной грани
.
В шестиугольной пирамиде 6 таких граней, получаем площадь боковой поверхности:
.
ответ: 360.
Онлайн курсы ЕГЭ и ОГЭ
16.
а)
Диагональ BD — делит четырёхугольник на 2 произвольных треугольника: ΔBCD; ΔBAD.
Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как:
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны: