Задача:
Длина окружности, вписанной в правильный треугольник, равна 12π см. Найдите периметр треугольника.
Чтобы найти периметр правильного Δ, нужно знать сторону; что найти сторону, нужно найти радиус вписанной окружности.
Дня нахождения радиуса окружности, воспользуемся формулой длины окружности и выразим из нее радиус:
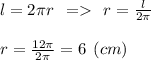
Теперь воспользуемся формулой радиуса вписанной окружности в правильный треугольник для нахождения стороны Δ:
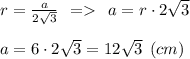
Осталось за малым — периметр правильного треугольника:
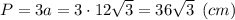
Периметр треугольника равен 36√3 см.
Площадь сектора:
Длина дуги сектора: