В треугольнике ABC AC= BC, K - точка пересечения биссектрис треугольника, а O - точка, равноудаленная от всех вершин треугольника. Отрезок OK пересекает сторону AB в точке E и точкой пересечения делится пополам. Найдите углы треугольника ABC.
------
Точка К равноудалена от сторон треугольника, поэтому является центром вписанной окружности.
Точка О - равноудалена от вершин треугольника и является центром описанной окружности. Точка К лежит на высоте и медиане к АВ ( на срединном перпендикуляре), точка О лежит на срединном перпендикуляре к АВ, поэтому С, К, Е и О принадлежат одной прямой СО.
Т.к. отрезок КО пересекает АВ, точка О расположена вне треугольника.
Высота и медиана СЕ ⊥ АВ и делит его пополам.
Соединим точки К и О с вершинами А и В.
В получившемся четырехугольнике АКВО отрезки АЕ=ВЕ, КЕ=ОЕ.
Треугольники, на которые КО и АВ делят этот четырехугольник, прямоугольные и равны по двум катетам.
Следовательно, АК=ВК=ВО=АО, и АКВО - ромб. АВ - его диагональ и делит его углы пополам.
Пусть ∠ЕАО=α, тогда ∠КАЕ=α, а, так как АК - биссектриса угла САВ, то ∠САК=∠ЕАК, и ∠САЕ=2α.
∆СОА - равнобедренный ( по условию ОА=ОС=ОВ).
∠ОСА=∠ОАС=3α.
Сумма острых углов прямоугольного треугольника равна 90°.
В ∆ СЕА ∠САЕ+∠АСЕ=5α.
5α=90°, откуда α=90°:5=18°
∠САВ=∠СВА=2•18°=36°
∠АСВ=180°-2•36°=108°.

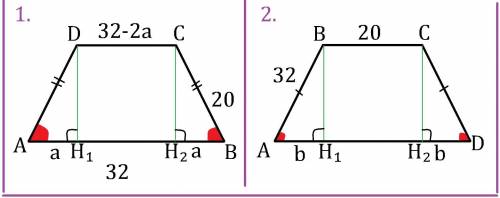
Угло при нижнем основании равнобедренной трапеции меньше 90°, а при верхнем больше 90°, поэтому ∠A = 60° - угол основания.
Нам неизвестно какая сторона боковая, известно только то, что они смежные. Поэтому решим два варианта.
1. AB - нижнее основание.
H₁, H₂ ∈ AB; DH₁ , CH₂ ⊥AB ⇒ DH₁ ║ CH₂
ΔADH₁ = ΔCBH₂ - по гипотенузе и острому углу т.к. трапеция равнобедренная.
AH₁ = H₂B - как соответственные стороны равных Δ.
∠H₂CB = 90° - ∠CBH₂ = 90° - 60° = 30° - как острые улг. в прямоугольном Δ.
H₂B = BC/2 = 20/2=10 - как катет лежащей напротив угла в 30° в прямоугольном Δ.
H₁H₂ = 32 - 10*2 = 12 = т.к. DH₁ ║ CH₂ и DH₁ = CH₂ - как соответственные стороны равных Δ.
P - периметр.
P = AB+ 2BC + CD = 32 + 40 + 12 = 84.
ответ: 84.
2. AB - боковая сторона.
H₁, H₂ ∈ AD; BH₁ , CH₂ ⊥AD ⇒ BH₁ ║ CH₂ ⇒ BH₁ = CH₂ - как параллельные отрезки заключённые между параллельными прямыми, поэтому BCH₂H₁ - прямоугольник ⇒ H₁H₂ = BC = 20.
ΔABH₁ = ΔCDH₂ - по гипотенузе и острому углу т.к. трапеция равнобедренная.
AH₁ = H₂D - как соответственные стороны равных Δ.
∠ABH₁ = 90° - ∠BAH₁ = 90° - 60° = 30° - как острые улг. в прямоугольном Δ.
AH₁ = AB/2 = 32/2=16 - как катет лежащей напротив угла в 30° в прямоугольном Δ.
BC = AD т.к. BH₁ ║ CH₂ и BH₁ = CH₂ - как соответственные стороны равных Δ.
AD = 20 + 16·2 = 52
P - периметр.
P = 2AB + BC + DA = 64 + 20 + 52 = .
ответ: 136.
38,8 см
Объяснение:
КХ=15,2 см
ХТ=23,6 см
КТ=КХ+ХТ=15,2+23,6=38,8см.
DM=KT=38,8см