∠ADB = 90°; ∠ABD = 40°; ∠ВАD = 50°;
Объяснение:
В равнобедренном треугольнике медиана BD, проведённая из вершины В на основание АС является биссектрисой ∠В и высотой.
Поэтому ΔABD - прямоугольный и ∠ADB = 90° (BD - высота)
∠ABD = 0.5 ∠B = 0.5 · 80° = 40° (BD - биссектриса ∠В)
По свойству углов треугольника
∠ВАD = 180° - (∠ADB + ∠ABD) = 180° - (90° + 40°) = 50°.
Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
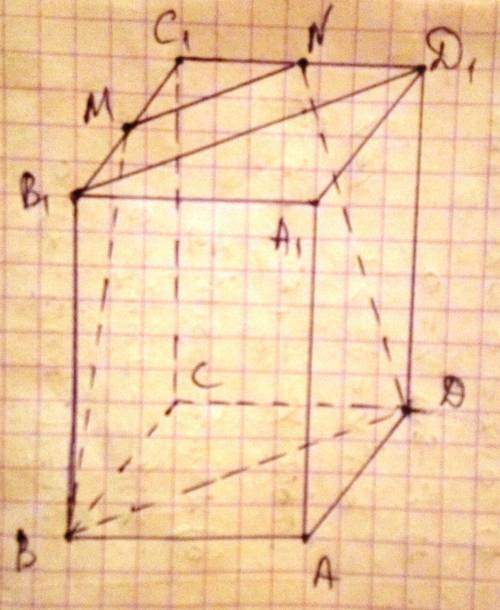
Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.

Відповідь: 40°, 50°, 90°
Якщо ∠В=80°, то ∠А+∠С=180-80=100°.
∠А=∠С=100:2=50° за властивістю кутів при основі рівнобедреного трикутника
ΔАВD - прямокутний за визначенням висоти трикутника,
ВD - також і бісектриса ∠В, за властивістю висоти рівнобедреного трикутника, отже, ∠АВD=80:2=40°
Отже, ∠А=50°, ∠АВD=40°, ∡ВDА=90°