(1) Сумма углов треугольника равна 180°.
1. Рассмотрим ΔAOC: AO=OC - по условию ⇒ ΔAOC - равнобедренный; По условию (1) найдем углы при основании. ∠А=∠С=(180°-128°):2=26°
2. Рассмотрим ΔAOB: AO=OB - по условию ⇒ ΔAOB - равнобедренный; По условию (1) найдем углы при основании. ∠A=∠B=(180°-96°):2=42°
3. Рассмотрим ΔBOC: BO=OC - по условию ⇒ ΔBOC - равнобедренный; По условию (1) найдем углы при основании. ∠B=∠C=(180°-136°):2=22°
4. Рассмотрим ΔABC:
∠A=42°+26°=68°
∠B=42°+22°=64°
∠C=22°+26°=48°
⇒ ∠A - наибольший угол ΔABC.
ответ: 68°
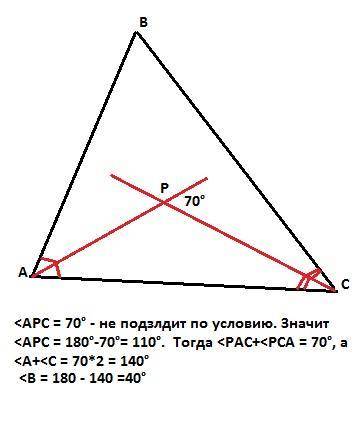
Третий угол треугольника равен 40°.
Объяснение:
Пусть в треугольнике АВС биссектрисы углов А и С пересекаются в точке Р. Тогда, если угол между биссектрисами АРС равен 70°, то на сумму двух других углов в треугольнике АРС остается 180-70 = 110°.
Это сумма половин углов А и С треугольника АВС. Тогда сумма углов А и С должна быть равна 220°, что противоречит свойству треугольника: сумма внутренних углов должна быть равна 180°.
Следовательно, нам дан угол между биссектрисами, смежный с углом АРС, то есть угол АРС = 180° - 70° = 110°. И тогда сумма половин углов А и С равна 70°, сумма целых углов А и С равна 140°, а третий угол треугольника АВС равен 180° - 140° = 40° (по сумме внутренних углов треугольника).
Найдите углы параллелограмма, если один из них на 28° меньше другого. Решение: Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°. Пусть один угол – х, другой – х-26, тогда: х+(х-26)=180; х+х-28=180; 2х-28=180; 2х=180+28; 2х=208; х=208÷2; х=104 – это один угол, тогда, х–28=104–28=76. Противоположные углы параллелограмма равны. ответ: углы параллелограмма равны: 104°; 104°; 76°; 76°. Проверка: 104+104+76+76=360. Равенство выполнено, значит, углы параллелограмма найдены верно.