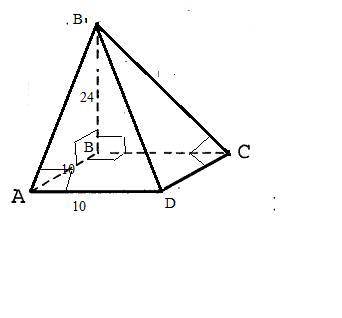
Основанием пирамиды является квадрат со стороной 10 см. Одно боковое ребро перпендикулярно плоскости основания и равно 24 см.
Вычисли площадь боковой поверхности.
Объяснение:
1)S(бок)=S(МВА)+S(МВС)+S(МАD)+S(МСD).
2)ΔМВА=ΔSМВС как прямоугольные по двум катетам⇒S(МВА)=S(МВС)=1/2*24*10=120 (см²).
Найдем МС= МА=√(24²+10²)=√676=26(см)
3)Т.к. прекция ВА⊥AD, то и наклонная МА⊥AD⇒ΔМAD-прямоугольный.
Т.к. прекция ВС⊥СD, то и наклонная МС⊥СD⇒ΔМСD-прямоугольный.
S(МАD)=S(МСD) как площади равных прямоугольных треугольников по катету и гипотенузе .
S(МАD)=S(МСD)=1/2*10*26=130 (см²)
4)S(бок)=2*120+2*130=500 (см²)
как то так вроде
Объяснение:
Дано: триугольник АВС, угол А=90°
АВ=14 см
ВС=40 см
угол В=30°
нужно найти: Р-?
теорема: стенка лежащая напротив угла 30° в прямоугольном триугольнике, будет равна половине гипотенузы
значит АС=40:2=20см
Периметр это сумма длин всех стенок
P=AB+BC+AC
P=14+40+20=74см
ответ: Р=74см