
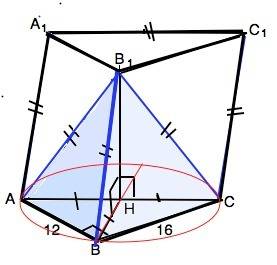
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
Найди длину вектора |x+y|. если |x| =3, |y| =4, а угол между векторами x и y равен 120°,
Решение.
Найдем сумму векторов по правилу параллелограмма , получим .
.
Вектор ОА=ВС( их длины равны и они сонаправлены )
Найдем длину отрезка ОС из ΔВОС . В нем ∠В=180°-120°=60°, ОВ=4, ВС=3 . По т. косинусов ОС²=ОВ²+ВС²-2*ОВ*ВС*cos(∠B),
ОС²=16+9-2*4*3*cos60°, cos60°=0,5 ;
ОС²=25-12 , ОС=√13 ⇒ |OC|=