
10 см
Объяснение:
Дано: ΔАВС - прямоугольный, ∠С=90°, ВD - медиана, BD=2√13 cм, АС=8 см. АВ - ?
Если в условии дана медиана треугольника, я решаю задачу, достроив треугольник до параллелограмма. Теорема об удвоении медианы:
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
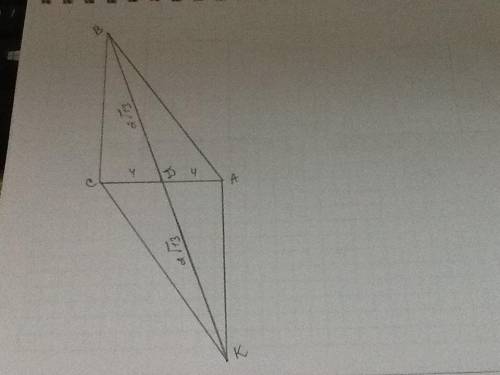
Продлеваем медиану на такую же длину и строим параллелограмм АВСК, где диагональ АС=8 см, диагональ ВК=2√13+2√13=4√13 см.
Тогда АС²+ВК²=2(АВ²+ВС²).
208+64=2(АВ²+ВС²)
272=2(АВ²+ВС²)
АВ²+ВС²=136.
Вернемся к ΔАВС. По теореме Пифагора
АВ²+ВС²=136
АВ²-ВС²=64 (т.е. АС²)
2АВ² = 200; АВ²=100; АВ=10 см.
ответ: 29°
Объяснение:
Сумма углов треугольника равна 180, таким образом:
∠ABC = 180 - 16 - 74 = 90
По свойству высоты, прямая, выходящая из вершины угла образую перпендикуляр с противоположной стороной, тогда:
∠MBC + ∠BCM + ∠CMB = 180 => ∠MBC = 180 - 74 - 90 = 16
По свойствам, медиана делит угол выхода пополам, а потому:
∠KBC = 90 / 2 = 45
Отсюда: ∠KBM = 45 - 16 = 29
Убедимся, что все верно:
∠ABC = ∠ABK + ∠KBM + ∠MBC = 45 + 29 + 16 = 90 - что и требовалось доказать.