ΔABN=ΔCDK по катету и гипотенузе, AB=DC /противолежащие стороны прямоугольника равны/, KD=BN /как равные высоты в равных треугольниках АВС и АDC, на которые их разбивает диагональ АС/
Отсюда следует, что AN=СК.
Рассмотрим Δ АВС , в нем ВN²=(AN*NC) по свойству высоты, проведенной из вершины прямого угла на гипотенузу. Пусть AN=х; х>0, тогда NC=(9+х); 36=х*(9+х); х²+9х-36=0; По Виета х=-12, х∈∅, х=3, Значит, АС=2*х+9=2*3+9=9+6=15/см/
Площадь прямоугольника найдем как сумму площадей двух одинаковых прямоугольных треугольников АВС и АDC. 2*(АС*ВN/2)=15*6=90/см²/
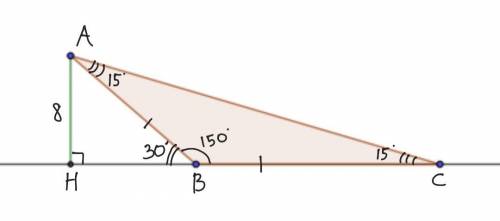
Дано: ΔABC - равнобедренный, АС - основание, АВ=ВС, ∠В=150°, АН - высота, АН = 8 е.д.
Найти: BC.
Решение.
Поскольку треугольник тупоугольный, а высота проведена из острого угла, то высота принадлежит продолжению противолежащей стороны.
Поэтому рисуем продолжение прямой ВС и высоту АН, проведённую к нему.
В ΔАНВ: ∠НВА = 180°-150°= 30° (как смежные).
АНВ - прямоугольный треугольник (АН ведь высота) с гипотенузой АВ.
В прямоугольном треугольнике, если острый угол равен 30°, то противолежащий этому углу катет равен половине гипотенузы.
АН=½АВ.
АВ= 2АН.
АН по условию 8, тогда АВ= 2×8=16.
ΔАВС - равнобедренный, АВ=ВС. Значит, ВС=16 е.д.
ответ: 16 е.д.
Половина диагонали и будет радиусом описанной окружности...
получили два равнобедренных треугольника с боковыми сторонами = R
в одном треугольнике угол при вершине 30 градусов (это угол между диагоналями), в другом 120 градусов (смежный с ним)...
осталось найти основания треугольников (это стороны прямоугольника)...
по т.синусов
из одного треугольника: a/sin30 = R/sin75
из второго треугольника: b/sin150 = R/sin15
Sпрямоугольника = ab = (Rsin30/sin75)(Rsin150/sin15) =
R^2sin30sin(180-30) / (sin(90-15)sin15) = R^2 / (4cos15sin15) = R^2 = 144
(т.к. Sкруга = pi*R^2 = 144pi => R^2 = 144)