Проведём от вершин верхнего основания высоты ВН иСМ
Дальше для простоты я обозначаю всё малыми буквами.
ΔАСМ прякоугольный, угол САМ=30⁰, значит
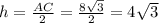см, как катет, лежащий против угла в 30⁰
Из ΔАСМ по т. Пифагора находим АМ:
Из вершины А поднимем перпендикуляр до пересечения в точке О с продолжением основания ВС.
ΔАОВ=ΔСМD по равен по певому признаку равенства прямоугольных треугольников (по катету и гипотенузе; хотя там можно и больше признаков найти).
Значит получаем основное соотношение для решения задания:
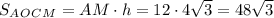см²
Находим сумму оснований трапеции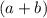 
из соотношения:
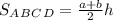
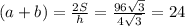см
Ну и, поскольку знаем, что
Средняя линия трапеции параллельна основаниям и равна их полусумме, то:
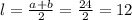см
Как "Лучшее решение" отметить не забудь, ОК?!.. ;)))
в равнобедренном треугольнике, высота проведённая к основанию, является медианой, поэтому основание делится на 2 равных отрезка по 5 см. По теореме Пифагора найдём боковую сторону
корень из 5^2+5^2= корень из25+25= корень из25*2=5 корень из2
найдём площадь треугольника, она равна половине произведения основания и высоты, поэтому S=1/2*a*h=1/2*10*5=5*5=25см^2
эту же площадь можно вычислить по другому
S=abc/4R, отсюда
R=abc/4S=10*5 корень из2*5 корень из2/4*25=10*25*2/100=5
эту же площадь можно вычислить как половина произведения периметра на радиус вписанной окружности S=1/2*P*r, r=2*S/P
P=10+2*5 корень из2=10+10 корень из2=10(1+ корень из 2)
r=2*25/10(1+ корень из 2)=5/(1+ корень из 2)=5*(1- корень из 2)/(1+ корень из 2)(1- корень из 2)=5( корень из 2-1)
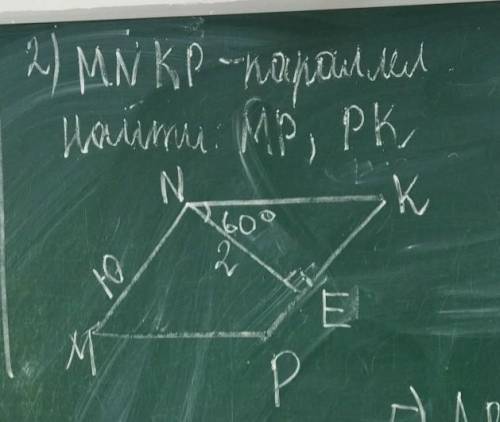
Объяснение:
РК=NM=10
NK=NE/cos60=2/0,5=4
MP=NK