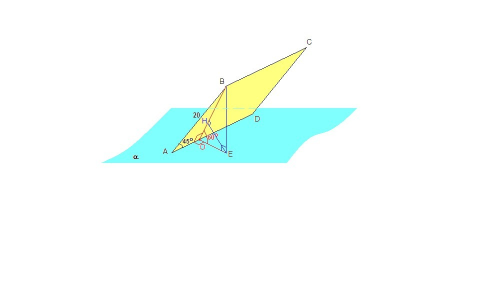
Проведем ВО⊥AD, ВО - наклонная к плоскости α, ЕО - ее проекция, значит ЕО⊥AD по теореме, обратной теореме о трех перпендикулярах. Тогда
∠ВОЕ = 60° - линейный угол двугранного угла ВADE.
Проведем ЕН⊥ВО.
AD⊥(ОВЕ) как ребро двугранного угла, значит AD перпендикулярен любой прямой, лежащей в этой плоскости, ⇒ ЕН⊥AD,
ЕН⊥ВО по построению, ⇒ ЕН⊥(АВС). ЕН - искомое расстояние.
ΔАВО: (∠АОВ =90°) ВО = АВ · sin45° = 20 · √2/2 = 10√2 см
ΔBOE: (∠BEO = 90°) BE = BO · sin60° = 10√2 · √3/2 = 5√6 см
EO = BO · cos60° = 10√2 · 1/2 = 5√2 см
EH = BE · EO / BO = 5√6 · 5√2 / 10√2 = 5√6/2 см
1. По теореме косинусов в треугольнике ВСD находим ВD = корень квадратный из (4 + 12 + 12) = корень квадратный из 28 = 2 корня квадратных из 7.
2. Проведем ВН перпендикулярно АD и заодно СМ перпендикулярно АD, для ясности.
в треугольнике СМD (прямоугольном) СМ = 1/2 СD = корень квадратный из 3, как катет лежащий против угла в 30 градусов.
Тогда и ВН = корень квадратный из 3.
3. В треугольнике ВКD (прямоугольном) по теореме Пифагора КD = корень квадратный из (28 - 3), то есть КD = 5.
В этом же треугольнике cosКDВ = КD / ВD = 5 / (2 корня квадратных из 7). - отношение прилежащего катета к гипотенузе.
4. В треугольнике АВD (прямоугольном по условию, т.к. АВ перпендикулярна к ВD), угол АDВ тот же, что и угол КDВ в треугольнике ВКD. Значит и косинус этого угла такой же.
таким образом cosКDВ = cosАDВ = ВD / АD (опять же отношение прилежащего катета к гипотенузе), отсюда находим АD.
АD = ВD / cosАDВ = (2 корня квадратных из 7) / (5 / (2 корня квадратных из 7)) = 28 / 5 = 5,6.
ответ: АD = 5,6.
Удачи! :-)
А1В1ВА - прямоугольная трапеция с основаниями АА1 и ВВ1, в которой ММ1 - средняя линия ММ1= (АА1+ВВ1) / 2 = (13+7)/ 2 = 10 м