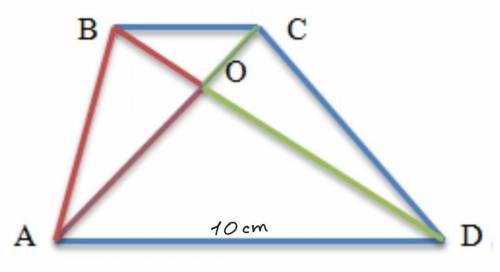
Нужно найти меньшее основание трапеции ABCD — это отрезок ВС.
Решение.
Согласно свойству диагоналей трапеции:
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения - подобны. Значит, ΔAOD~ΔBOC.
По условию Saod = 32 см², Sboc= 8 см².
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Saod / Sboc = k²;
32/8 = k²;
k²= 4;
k= 2 (-2 не подходит).
Коэффициент подобия треугольников AOD и BOC равен 2.
Соответственные стороны этих треугольников относятся и при делении равны коэффициенту.
Т.е. AD / BC = k.
AD=10 см по условию.
10 / ВС = 2;
2ВС=10;
ВС= 5 (см).
ответ: 5 см.
#4.
Для начала найдём высоту. Она равна среднему геометрическому между образованными отрезками(из гипотенузы) этой высотой.
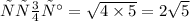
По теореме Пифагора найдём нужный нам катет обозначим его буквой х:
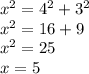
ответ:5.
#5.
Итак, высота равна среднему геометрическому между образованными отрезками(из гипотенузы) этой высотой,давайте буквой х обозначим часть гипотенузы, которую мы не знаем:
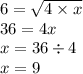
Итак, мы нашли неизвестную часть гипотенузы, но мы ещё не ответили на нужный нам вопрос, нам нужно найти полностью гипотенузу,для этого сложим части гипотенузы и мы её найдём:4+9=13.
ответ:13.
#6.
Решение и ответ во вложении.
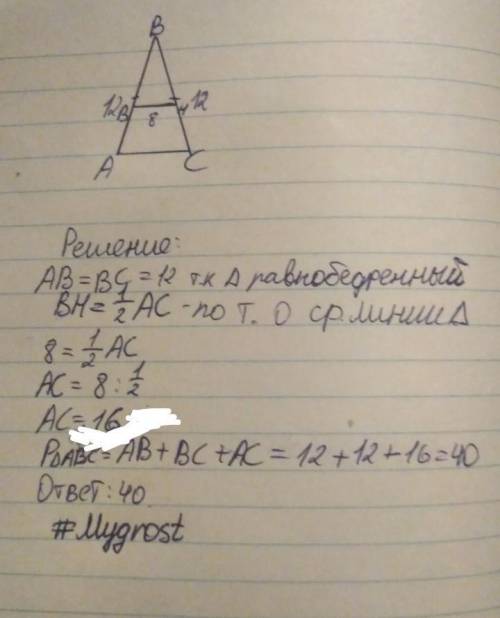
Пусть х – коэффициент пропорциональности. Тогда, стороны трапеции будут равны 4х, 5х, 5х, 8х. Составим уравнение: 4х+5х+5х+8х=44; 22х=44; х=44:22; х=2. Значит, 4х=4*2=8(см); 5х=5*2=10(см); 5х=5*2=10(см); 8х=8*2=16(см).
первая сторона – 8 см;
вторая сторона – 10 см;
третья сторона – 10 см;
четвёртая сторона – 16 см.