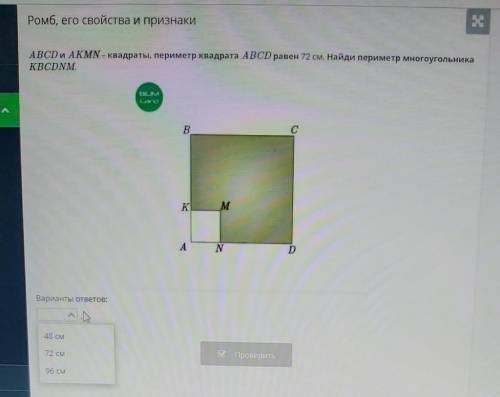
48 см
Объяснение:
1). Периметр ABCD = 72 см. Мы знаем, что стороны квадрата равны,значит одна сторона - это 72 : 4 = 18 см
2). Проведем диагональ BM и высоту ML. Получим два равных треугольника, а BK = 2 AK => KM + KA = 12 ( (⅓ * 18) * 2 ). Тогда периметр AKMN = 12 * 2 = 24 см
3). P kbcdnm = 72 см - 24 см = 48 см
ответ:дано АВС и А1В1С1
В=В1=90
А=А1
ВН перпенд АС
В1Н1 перпенд А1С1
ВН=В1Н1
доказать АВС=А1В1С1
док-во
очевидно, что углы с=с1
значит, треугольники подобны. Соответственно, подобны все величины, в том числе и соответствующие высоты. Но так как высоты равны, то коэфф. подобия равен 1 , соответственно все стороны подобны с коэфф. 1, т.е. равны. Отсюда, треугольники равны.
Можно докавзать чуть по-другому, но там дольше. Т.е. высоты разбивают на два треуг, потом в каждом треуг. сторона и углы равны, значит другие стороны равны. И т.д. и т.п. итог- треуг равны
Чертёж смотрите во вложении.
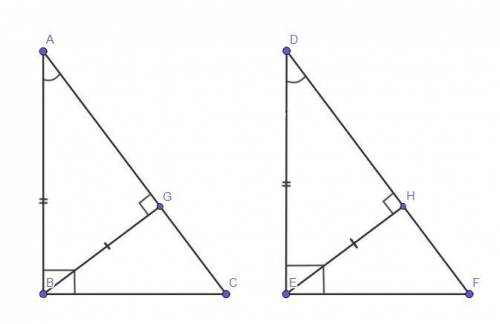
Дано:
ΔАВС - прямоугольный (∠АВС = 90°).
ΔDEF - прямоугольный (∠DEF = 90°).
ВG - высота ΔАВС.
ЕН - высота ΔDEF.
BG = EH.
Острые ∠ВАС = ∠EDF.
Доказать:
ΔАВС = ΔDEF.
Доказательство:
Рассмотрим ΔBAG и ΔEDH - прямоугольные (так как BG и EH - высоты и они перпендикулярны сторонам, к которым они проведены). Катеты BG = EH по условию (они катеты, так как лежат против острых углов в прямоугольном треугольнике), острые ∠ВАС = ∠EDF по условию, следовательно, прямоугольные ΔBAG = ΔEDH по катету и противолежащему острому углу.
В равных треугольниках против равных углов лежат равные стороны. В прямоугольных ΔBAG и ΔEDH ∠AGB = ∠DHE (так как они прямые), тогда, по выше сказанному, АВ = ED.
Рассмотрим ΔАВС и ΔDEF - прямоугольные. Катеты АВ = ED (по выше доказанному), острые ∠ВАС = ∠EDF (по условию), следовательно, прямоугольные ΔАВС = ΔDEF по катету и прилежащему острому углу.
ответ: что требовалось доказать.
паралеллограм у которого все стороны равны является ромбом