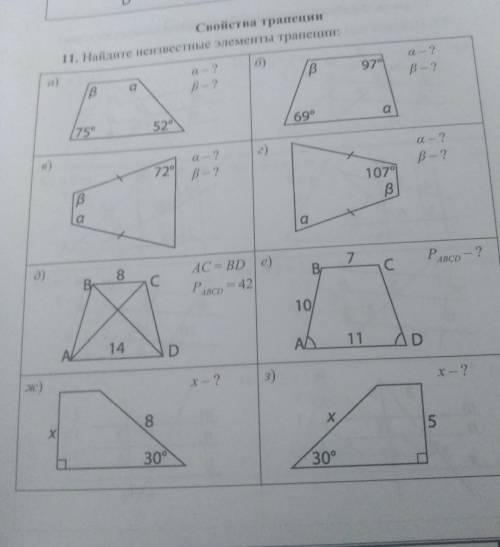
Площадь трапеции равна произведению её высоты на полусумму оснований ( среднюю линию).
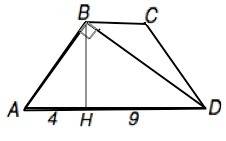
Обозначим трапецию АВСD, высоту - ВН. Тогда АН=4, DH=9
Высота равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности оснований, больший – их полусумме. ⇒
S=BH•HD
Треугольник АВD- прямоугольный.
Его высота – общая с высотой трапеции.
Высота прямоугольного треугольника, проведенная из прямого угла - среднее пропорциональное между отрезками, на которые она делит гипотенузу.
ВН²=АН•DH=4•9=36
BH=√36=6
S(трап)=6•9=54.
Объяснение: г) т.к. трапеция равнобедренная, то углы при основаниях равны, а, значит, β=107°, α и β прилежат к боковой стороне, поэтому их сумма равна 180°, значит, α=180°-β=180°-107°=73°
ж) если из вершины тупого угла провести к основанию высоту, то она будет равна х, и чтобы эту высоту найти, надо рассмотреть треугольник, в котором данная высота лежит против угла в 30°, а, значит, равна половине гипотенузы, равной 8 , т.е. х=8/2=4