
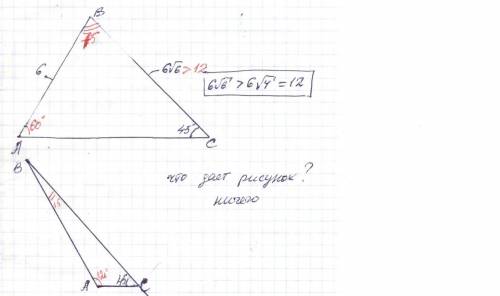
Найдите углы A и B треугольника ABC, если AB=12 см, BC=6√6 см, угол C= 45°.
ответ: 60° , 75° или 120° , 15° .
Объяснение:
По теореме синусов : BC / sin(∠A) =AB / sin(∠C ) ⇔
6√6/sin(∠A)=12/sin45°⇔sin(∠A) =6√6*sin45°/12=6√6 *(√2/2) / 12 = 3 /2 ⇒
∠A= 60° или ∠A= 120° . Оба верны ∠A > ∠C , т.к. BC > AB
( в треугольнике против большой стороны лежит большой угол )
* * * BC > AB : BC = 6√6 > 6√4 = 12 = AB * * *
∠B = 180° - (∠A+√C) → ∠B = 75° или ∠B = 15° см. лишнее приложение
66,66,48
Объяснение:
Внешний угол равен сумме двух углов несоседних с ним, тобишь сумме углов при основе. Поскольку треугольник у нас равнобедренный, то эти углы между собой равны и, чтобы найти каждый из них мы делим их сумму надвое
1) 132:2=66
Дальше просто за суммой углов треугольника находим третий угол.
2) 180-66-66=48
Или же мы можем найти третий угол другим тут сами выбирайте. Итак, угол при вершине и внешний угол смежные, то есть их сумма равна 180 градусов, поэтому просто:
2) 180-132=48
В принципе нет разницы как найдёте третий угол. Все равно что там по сути 180-132, что там) удачи
"C" я сам делал наугад и попал