ответ: Не верьте громоздким готовым формулам, они отучают думать
Объяснение:
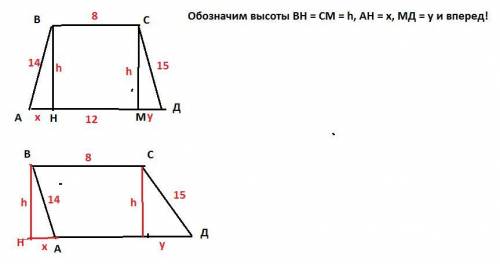
Трапеции бывают разные. Вот если мы применим рисунок со стандартной трапецией, то выяснится, что она не существует.
неизвестная будет отрицательная и прочие неприятности. Но на втором рисунке тоже трапеция, так как АД||ВС, а две другие стороны не параллельны. Вот его мы и решим.
Когда мы провели две высоты мы от основания отрезали отрезок
что у = АД - 8+х или у=4+х Это первое уравнение.
Из прямоугольных треугольников на рисунке выразим высоту, не спеша вдумчиво и применяя теорему святого Пифагора:
Из ВНА будет h² = AB² - x²
Из СМД будет h² = CД² - у² и так как левые части равны, приравняем и правые части АВ²-х² = СД² -у² или подставив значения боковых сторон 14²-х² = 15²-у² а отсюда уже
у²-x²=225-196 = 29 уравнение. Решив систему этих уравнений (я расписывать это здесь не буду, нудно) мы получим, что х=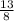
Тогда из треугольника ВНС
h² = 14² -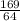 
= 13,9
И это решение верное.
Извини уж, под рукой ни листа бумаги, ни карандаша нет, так что решу только задачи в которых есть рисунок.
1) Угол 1 и 2 равны. Т.е. Угол 2 равен 135 градусам.
3) Угол Р равен 180 градусов(сумма всех углов любого треугольника) минус угол О 60 и угол N 90. 180-60-90 = 30 градусов равен угол Р.
В прямоугольном треугольнике катет лежащий напротив угла 30 градусов, равен половине гипотенузы, значит катет ON равен 8/2=4.
Далее по теоеме Пифагора найдем другой катет. PN^2=PO^2-ON^2
PN^2=64-16=48. Значит PN =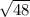
или 4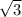
8) Треугольники PQH и QRH - прямоугольные, значит их площадь равна половине площади прямоугольника, со сторонами, равными катетам этих треугольников.
Площадь треугольника PQH = 9*12/2=54 Площадь треугольника QRH=12*16/2= 96.
Нужно найти площадь треугольника PQR= 54+96=150. ОТвет 150.
10) ML - средняя линия трапеции. Ее можно найти, посчитав полусумму оснований трапеции. Т.е. (BC+AD)/2.
ML=(7+15)/2=11. ответ 11.
Объяснение: