30 см
Объяснение:
Рассмотрим вложение.
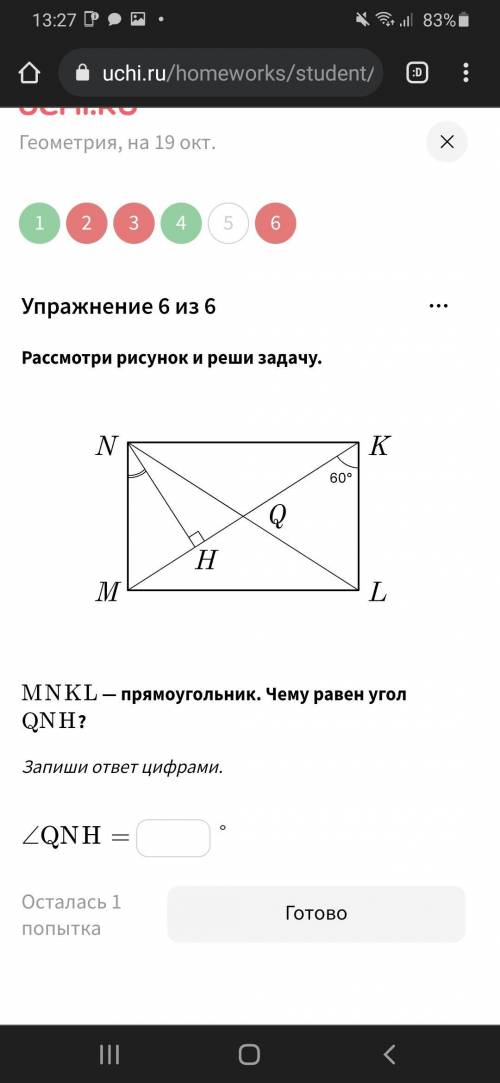
Нам дан ΔАВС: ∠А = 90°, ВС = 13 см
Пусть АВ = х см, тогда АС = х + 7 см. Воспользуемся т.Пифагора для нахождения стороны.
АВ² + АС² = ВС²
х² + (х + 7)² = 13²
х² + х² + 14х + 49 = 169
2х² + 14х + 49 - 169 = 0
2х² + 14х - 120 = 0 |:2
х² + 7х - 60 = 0
D = 7² - 4 * (-60) = 49 + 240 = 289 = 17²
x₁ = (-7 - 17)/2 = -24/2 = -12
x₂ = (-7 + 17)/2 = 10/2 = 5
т.к. сторона не может быть отрицательна, то АВ = 5 см, тогда
АС = 5 + 7 = 12 см
Чтобы найти периметр треугольника, надо сложить все стороны.
Р = АВ + ВС + АС = 5 + 13 + 12 = 30 см
ответ: 30°
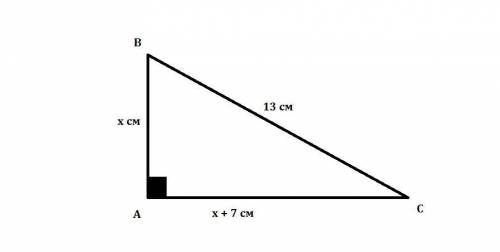
Объяснение: NMKL - прямоугольник. Диагонали прямоугольника равны и точкой пересечения делятся пополам. NL=MK, MQ=QK=QL. =>
∆ KQL – равнобедренный, углы при основании KL=60° =>
угол KQL=60°, угол NQH=60° равен ему (вертикальный).
Сумма острых углов прямоугольного треугольника 90°, поэтому искомый угол QNH=90°-60°=30°.
Или иначе:
∆ MQN=∆ KQL, – он равносторонний, NH- его высота, медиана и биссектриса.
Угол QNH=MNH=60°:2=30°.