Объяснение:
1) ∠KON = 180° - 78° = 102° (как смежный с ∠MOK)
x = ∠OKN = (180° - 102°) / 2 = 39° (ΔKON равнобедренный)
5) Дуга SNM = 180° (стягивает диаметр)
Меньшая дуга MN = 80°, т.к. на нее опирается вписанный угол в 40°
Следовательно x = 180° - 80° = 100°
2) Т.к. AO = OB, то ΔAOB равнобедренный. А т.к. угол при вершине O равен 60°, то он равносторонний. Отсюда x = 8.
6) Меньшая дуга MK = 360° - 180° - 124° = 56°
Вписанный угол опирающийся на эту дугу равен половине ее градусной меры:
x = 56° / 2 = 28°
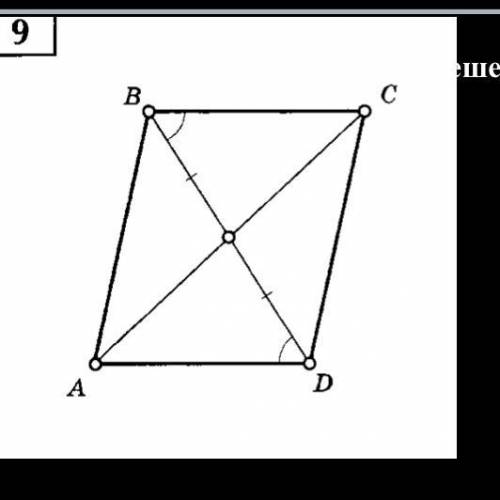
BO и BD диагонали, они равны
угол ОВС и угол АDО равны по условию и являются накрест лежащими, тогда ВС параллельна АД
угол ВОС и угол АОД равны как вертикальные
рассмотрим треугольники ВОС и АОД
эти треугольники равны по 2 признаку ( 2 угла и сторона), соответственно АД= ВС
Если АД=ВС и они параллельны, то этот четырёхугольник - параллелограмм по признаку Параллегограмма, чтд
Объяснение:
чтд - что и требовалось доказать
О - центр, точка на рисунке