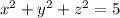1) Как называется утверждение которое нельзя доказать?
Аксиома.
2) Из теоремы "Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны" составьте обратную.
Меняем "если" и "то" местами: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Как называются прямые на плоскости, не имеющие общих точек?
Параллельными.
4) Если прямая a параллельна прямой b, и прямая а параллельна прямой с, то что можно сказать о прямых b и c?
Тогда b║c.
5) Изобразите: две параллельные прямые пересеченные секущей, отметьте числами 5 и 6 углы, которые являются односторонними.
См. рисунок.
6) О равенстве каких углов можно утверждать, если параллельные прямые пересечены секущей.
Тогда равны накрест лежащие углы: ∠1 = ∠7, ∠4 = ∠6
и равны соответственные углы: ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8.
3)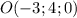
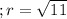
4)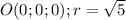
Объяснение:
Уравнение сферы в общем виде:
Пусть точка O - центр сферы. Координаты центра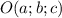 . r - радиус сферы.
. r - радиус сферы.
3)
4)