ответ: 3 см, 12 см.
Объяснение:
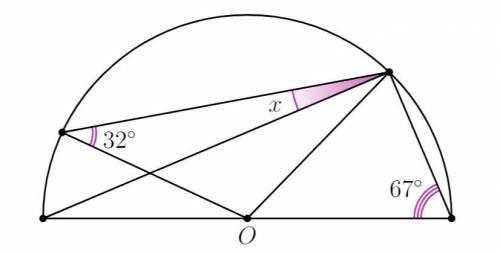
АВ = 11 см и АС = 16 см - наклонные к прямой а,
АН - перпендикуляр к прямой а, тогда
ВН и СН - проекции соответствующих наклонных.
Большей наклонной соответствует большая проекция.
Пусть ВН = х см, тогда СН = (х + 9) см.
Из прямоугольного треугольника АВН по теореме Пифагора выразим АН:
АН² = АВ² - ВН²
АН² = 11² - x² = 121 - x²
И выразим АН по теореме Пифагора из прямоугольного треугольника АСН:
AH² = AC² - CH²
AH² = 16² - (x + 9)² = 256 - (x² + 18x + 81) =
= 256 - x² - 18x - 81 = 175 - x²- 18х
Приравняем правые части получившихся равенств:
121 - x² = 175 - x²- 18х
18x = 54
x = 3
ВН = 3 см
СН = 3 + 9 = 12 см
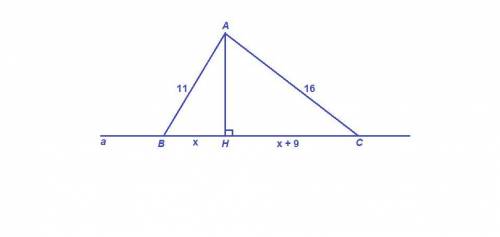
△ACD: ∠ACD=90 (опирается на диаметр AD). ∠CAD=90-67=23
OA=OC (радиусы), △AOC -р/б => ∠ACO=∠CAO=23
OB=OC (радиусы), △BOC -р/б => ∠BCO=∠CBO=32
∠BCO =∠BCA+∠ACO => 32 =x+23 => x=9°
Или
Внешний угол вписанного четырехугольника (ABCD) равен противолежащему внутреннему.
∠CBE=∠D =67
∠DAF=∠BCD =x+90
△AOB -р/б, ∠OAF=∠OBE (смежные с равными)
=> x+90=32+67 => x=9°