№1:  . №2:
. №2: 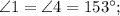
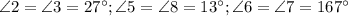 .
.
№1.
Пусть  , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна  .
.
 , по условию.
, по условию.
 и
и  - односторонние углы
- односторонние углы 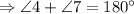
№2.
Обозначим данные прямые буквами 
Пусть  - секущая прямых
- секущая прямых  и
и 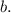
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
 и
и 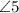 - накрест лежащие при пересечении
- накрест лежащие при пересечении  и
и  секущей
секущей  , однако
, однако 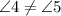 .
.

 и
и  - не параллельны.
- не параллельны.
============================================================
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна  ".
".
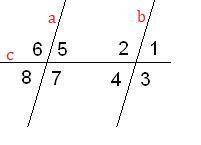
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и 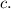
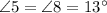 , по свойству вертикальных углов.
, по свойству вертикальных углов.
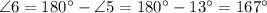 , по свойству смежных углов.
, по свойству смежных углов.
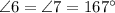 , по свойству вертикальных углов.
, по свойству вертикальных углов.
===========================================================
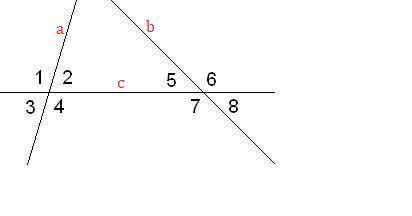
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и  .
.
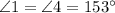 , по свойству вертикальных углов.
, по свойству вертикальных углов.
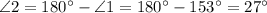 , по свойству смежных углов.
, по свойству смежных углов.
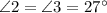 , по свойству вертикальных углов.
, по свойству вертикальных углов.
Объяснение:
Доказательство: Пусть даны две прямые a и b. Предположим, что они имеют более одной общей точки - точки M и N. Тогда через две точки M и N проходила бы не одна, а две прямые - прямые a и b. Но это противоречит аксиоме. Конец доказательства.
Что мне не нравится в доказательстве: Хорошо, мы доказали, что две разные прямые не могут иметь две общие точки. Но для меня ситуация выглядит так, что мы доказали только этот частный случай. А если мы возьмем три общие точки или больше? Не похоже, чтобы аксиома запрещяла, чтобы две разные прямые имели три общие точки.
Умом-то я понимаю, что если две прямые имеют более одной общей точки, то они являются одной и той же прямой. Но вот строго доказать, увы, не могу. И мне кажется, что для этого хватит все той же аксиомы. А вся моя проблема проистекает из-за неверного понимания самой аксиомы, которая скорее всего запрещяет и случаи с большим количеством общих точек.
МОЛОДЦЫ ДЕРЖИТЕСЬ УДАЧИ ВАМ -^-)