Хорошо, сведем задачу к нахождению диагонали трапеции т.к. есть формула S= d^2/2 * sinA где d- диагональ, синус угла 60 у нас есть он равен 1/2* корень из 3. Диагонали в равнобедр. трапеции образуют собой равнобедр. треугольники AOD и BOC рассмотри треугольник ВОС: угол ВОС равен 180- 60= 120, тогда углы при основании равны по 30 (углы ОСВ и ОВС) далее возьмем прямоугольный треугольник АНС где АН- высота: угол АСН мы нашли он равен совпадающему углу ОСВ и равен 30 тогда угол НАС равен 180-90-30=60 АН=2 найдем сторону НС: по формуле НС = АН*tgА= 2* tg HAC= 2 * tg 60 = 2* корень из 3= 2 корня из 3 окей, далее найдем АС она же является диагональю трапеции: АС= НС/sin НАС= 2 корня из 3/ ( 1/2* корень из 3) = 4 готово, осталось посчитать: S = АС^2 /2 * sin 60= 8* корень из 3 /2 = 4 корня из 3 см в квадрате
Даны векторы k(-1;2), s(5;-12), c(2;x). Найдите: a)cos(∠k, s) ; b) число x, если k и c - коллинеарные; c) число x, если s и c - перпендикулярны.
Объяснение:
a)Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин.
Найдем длины векторов:
Длина вектора |k|=√( (-1)²+2²)=√(1 +4)=√5,
Длина вектора |s|=√( 5²+(-12)²)=√(25+144)=√169=13,
Скалярное произведение k*s=-1*5+2*(-12)=-5-24=-29
cos(∠k, s)= .
b) Два вектора коллинеарные ,если их координаты пропорциональны, значит для k(-1;2),c(2;x) :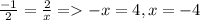 ;
;
c)Вектора перпендикулярны , если их скалярное произведение равно нулю : ⇒ 12x=10 , x=
⇒ 12x=10 , x=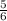 .
.