
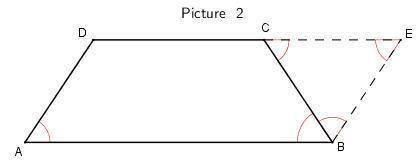
2) Из вершины D продлим сторону до пересечения на продлении стороны BC, так что AB ║ DE, т.е. ABED — параллелограмм.
∠A = ∠E = 60° (противоположные углы у параллелограмма равны)
Так как AB = CD ⇒ ED = CD ⇒ ∠ECD = ∠CED = ∠CDE = 60°, т.е. треугольник CDE — равносторонний ⇒ CD = CE = ED = 32
Тогда AD = BC + CE = 20 + 32 = 52
P = 20 + 32 + 32 + 52 = 136
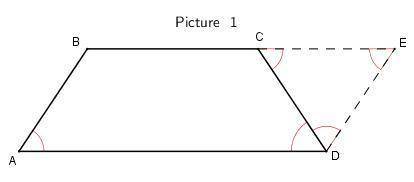
Рисунок 2.
Аналогично решению из рисунка 1, достроим до параллелограмма ADEB, AD ║ EB, мы имеем что ΔCEB - равносторонний, т.е. CE = CB = EB = 20, тогда CD = AB - CE = 32 - 20 = 12.
P = 12 + 20 + 20 + 32 = 84
3)
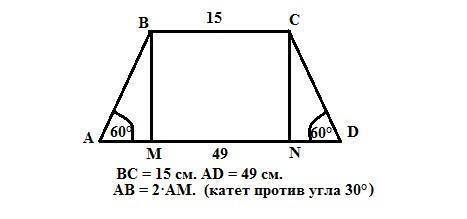
Дано: равнобедренная трапеция АВСD.
АВ=СD.
Меньшее основание ВС=15 см. Большее основание AD=49 см. Острые углы D=A=60° (трапеция равнобедренная).
Найти: периметр трапеции Р=?
Опустим перпендикуляры к большему основанию СN и ВM. МN=BC=15 cм, АМ=АN=(49-15):2=17 см.
Рассмотрим треугольник АВМ. Угол А=60°, следовательно угол В=30°, т.к. сумма острых углов прямоугольного треугольника=90°.
Катет лежащий против угла в 30° равен половине гипотенузы, значит АВ = 2·АМ = 2*17=34 см.
Теперь известны все стороны трапеции АВ=СD=34см, ВС=15см, АD=49см.
Р=34*2+15+49=132 см.
4) На фото.
7) На Фото
8)
DC║KB - как отрезки лежащие на основании трапеции.
DK║CB - по условию, поэтому DCBK - параллелограмм, значит DK=CB и ∠KBC=∠KDC=∠2; ∠AKD=∠KBC - как соответственные.
∠DAB=∠ABC - как углы при основании трапеции. В итоге в ΔADK все 3 угла равны, значит он равносторонний.
KB=DC=14,15 см как противоположные стороны параллелограмма.
AK=AB-KB=27,65см - 14,15 см=13,5 см. AD=AK=13,5 см - как стороны равностороннего треугольника. AD=BC - по условию.
P(ABCD) = AB+BC+CD+DA = 27,65см+13,5см+14,15см+13,5см = 41,8см+27см = 68,8см
8)


1.Фигуры на плоскости
2 Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.
3Рассмотрим ΔBAO и ΔOCD
AO=OC - по условию
BO=OD - по условию
∠AOB=∠COD - вертикальные
⇒ ΔBAO=ΔOCD - по первому признаку (2 стороны и угол между ними)
Билет №2.
1. геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла)Это угол равный 180..Любой угол разделяет плоскость на 2 части. Если угол неразвёрнутый, то одна из частей называется внутренней, а другая внешней областью этого угла.Если угол развёрнутый, то любую из двух частей, на которые она разделяет плоскость можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области, так же называют углом.От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°,и только один.
2. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.
3.т. к. Сумма углов треугольника 180°,
значит третий угол 180-32-57=91°
Билет №3.
1.Равносторонним треугольником называется треугольник, у которого все его стороны равны.1) Все углы равностороннего треугольника равны по 60º.2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают,3)Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин.6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности.7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе.8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности.
2.Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными.
3. Возьмем отрезок АД за х, тогда ОА = х+8: х+х+8=24. 2х=16, х=8