У прямой y = -8x + 9 находим точку, которая принадлежит оси ординат.
При этом х = 0, тогда у = 9. Точка А(0; 9).
Для параллельной прямой угловой коэффициент сохраняется.
у = 4х + в. Подставим координаты точки А, через которую должна пройти прямая.
9 = 4*0 + в, отсюда в = 9.
ответ: у = 4х + 9.
Это общее решение такого рода задания, Для данной задачи можно было решить проще, так ка слагаемое "в" в уравнении прямой равно координате "у" в точке пересечения прямой оси Оу. У нас это 9.
С учётом равенства угловых коэффициентов сразу получаем уравнение параллельной прямой у = 4х + 9.
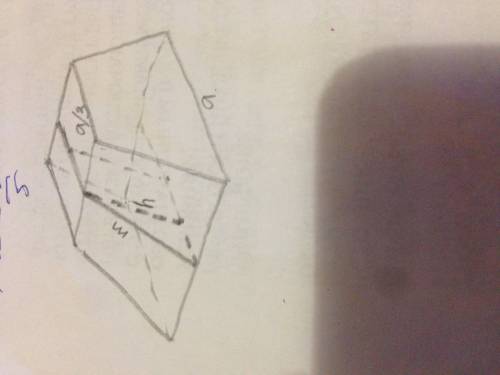
Через точку P проведем плоскость, параллельную грани AA1D1D.
Отсечем прямоугольный параллелепипед PQRTB1C1CB.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
PB1=2, BB1=B1C1=3
PC =√(4+9+9) =√22 (см)