ответ: ВД приблизительно 73,32см
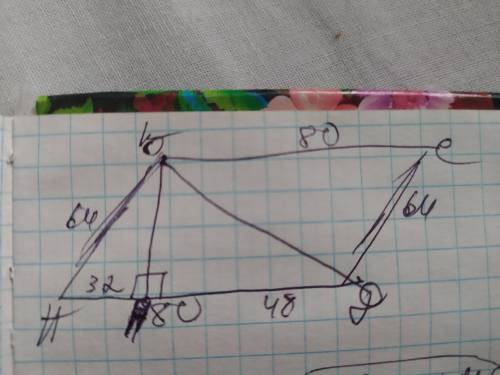
Объяснение: так как нам известно, что сторону АД =80 ° делит высота ВН, отсекая от неё отрезок 32см, то второй отрезок будет: 80-32=48см;
АН=32см; НД=48см. Рассмотрим ∆АВН- он прямоугольный и ,зная в нём две стороны, найдём по теореме Пифагора высоту ВН:
ВН²=64²-32²=4096-1034=3072=√3072
ВН=√3072см. Теперь рассмотрим ∆ВДН - он тоже прямоугольный и, зная высоту ВН мы можем найти диагональ ВД- расстояние между вершинами тупых углов по теореме Пифагора:
ВД²=48²+3072= 2304 +3072=5376
ВД=√5376=√256×√21=16√21(см). Если округлить до сотых будет приблизительно 73,32(см)
18
Объяснение:
Рассмотрим треугольник DCM: прямоугольный, т.к. стороны DC и CM лежат в перпендикулярных плоскостях. DC дана, CM = BL т.к. это противолежащие стороны параллелограмма BLMC. По условию между ни ми прямой угол, то есть они есть катеты, а требуемая сторона MD - гипотенуза этого треугольника. Тогда:
MD = √(DC² + CM²) = √(14² + (8√2)²) = √324 = 18