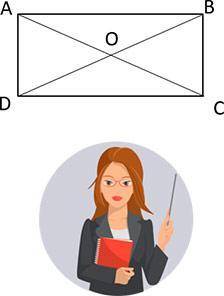
1. Соединим точки С и D с центром. Тогда треугольники AOD и ВОС равнобедренные (OA = OB = OC = OD как радиусы), ⇒
∠1 = ∠2 и ∠3 = ∠4.
∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АВ. Но тогда в этих треугольниках равны и углы при вершине О. Значит треугольники AOD и ВОС равны по двум сторонам и углу между ними, ⇒
AD = BC.
2. Точки, находящиеся на данном расстоянии от данной прямой а, будут расположены на прямой, параллельной прямой а (красные прямые). В зависимости от расположения прямых задача может иметь одно решение (1), два решения (2) и не иметь решения (3).
1)нет 2)да . . .
. . . . . .
81 см
Объяснение:
В прямоугольники диагонали равны и точкой пересечения делятся пополам. Поэтому АС= BD=54 cм и АО=OD=54:2=27 см
Так как ABCD – прямоугольник, значит ∠ADC=90°, поэтому ΔADC-прямоугольный с гипотенузой АС, а катет AD лежит против
∠ACD = 30°, значит AD=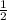 AC=27 cм
AC=27 cм
периметр треугольника AOD=AO+OD+AD=27+27+27=81 см