В решении этой задачи применима теорема Пифагора.
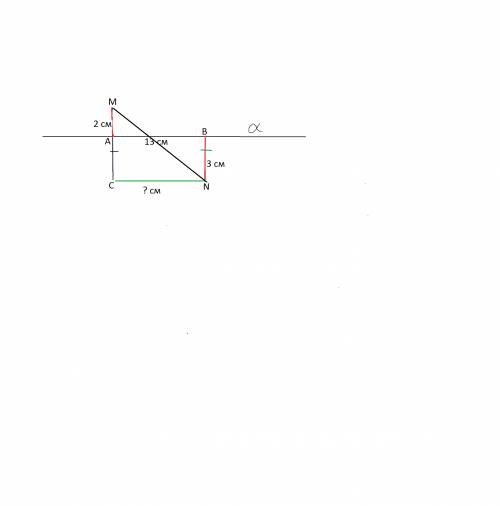
Смотрите рисунок, данный во вложении.
Если продолжить расстояние от точки А - проекции М на прямую α -
на длину расстояния от точки N до ее проекции В,
и соединить конец С этого отрезка с N,
получим прямоугольный треугольник MСN,
в котором известны гипотенуза MN=13 см,
и меньший катет МС=2+3=5 см
Если знаете несколько из Пифагоровых троек, а это как раз такая тройка (13,5,12), то, возможно, догадаетесь, что СN =12 см
По теореме Пифагора:
СN²=MN²- МС²= 169-25=144
СN=12 см
АВ=СN=12 см
ответ: Искомое расстояние равно 12 см
1) S(∆ABC)=√21см²
2) Расстояние от точки А до точки D; AD=√37см
Объяснение:
∆АВС- прямоугольный треугольник, по условию.
ВС; ВА- катеты.
АС- гипотенуза.
По теореме Пифагора
ВА=√(АС²-ВС²)=√(5²-2²)=√(25-4)=√21см.
S(∆ABC)=1/2*BA*BC=1/2*2*√21=√21см².
∆DBA- прямоугольный треугольник
DB; BA- катеты.
DA- гипотенуза.
DA=√(DB²+BA²)=√(4²+(√21)²)=√(16+21)=
=√37см