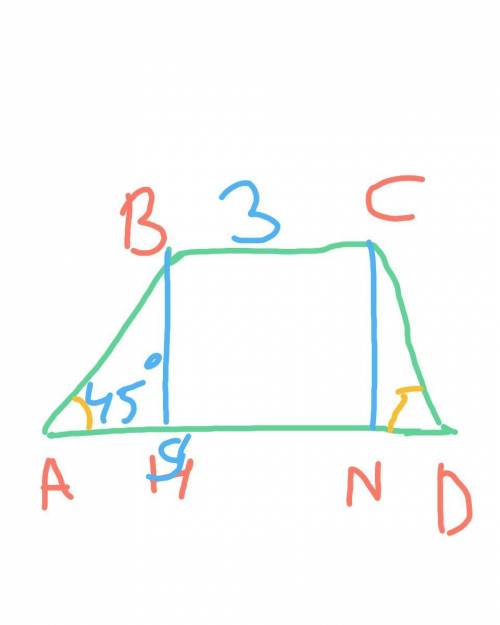
Дано: ΔABC - равнобедренный, АВ=ВС, AD - биссектриса, BD= 10 см, CD= 15 см.
Найти: Рabc.
Решение.
Так как по условию BD= 10 см, CD= 15 см, то ВС= BD+CD= 10+15= 25 (см).
Поскольку АВС - равнобедренный треугольник, то AB=BC= 25 см.
По свойству биссектрисы угла треуголька:
биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
Т.е. AB : BD = AC : CD;
25:10= AC:15;
AC= 25•15 : 10;
AC= 37,5 (см).
Находим периметр треугольника АВС:
Рabc = AB+BC+AC= 25+25+37,5= 87,5 (см).
ОТВЕТ: 87,5 см.
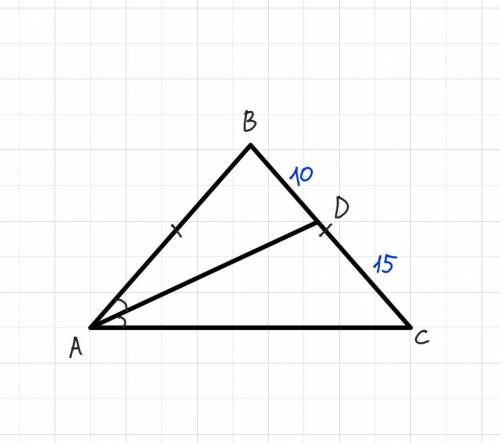
Дано:
АBCD - равнобедренная трапеция;
АВ = СD (боковые стороны);
BC (основание) = 3;
AD (основание) = 9;
Угол DAB = углу ADC = 45°;
BH и СN - высоты АВСD.
Найти: S (ABCD).
1) Рассмотрим прямоугольник HBCN (т. к. BH и CN - высоты АВCD):
▪ВС=HN=3 см (по свойству противоположных сторон параллелограмма).
2) AH = DN = (AD - HN) : 2 = (9 см - 3 см) : 2 = 6 см : 2 = 3 см.
3) Угол АВС = углу BCD (т. к. ABCD - равнобедренная трапеция) = (360° (сумма всех углов четырёхугольника) - угол DAB - угол ADC) : 2 = (360° - 45° - 45°) : 2 = 270° : 2 = 135°.
4) Рассмотрим прямоугольный треугольник АВН (т. к. ВН - высота ABCD):
▪Угол АВН = угол АВС - угол СBH = 135° - 90° (т. к. ВН - высота ABCD) = 45° => угол DAB = углу АВН = 45° => АВН - равнобедренный треугольник с прямым углом Н => АВ = BH.
5) ...