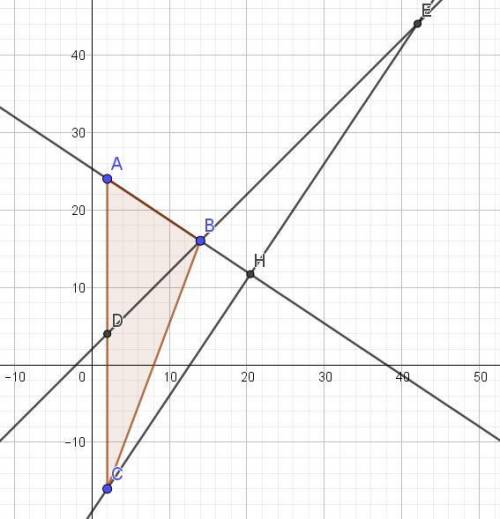
Даны координаты точек : А (2;24), В (14;16), С (2;-16).
а) Середина АС - точка М((2+2)/2=2; (24-16)/2=4) = (2; 4).
Уравнение ВМ: (х - 14)/(2 - 14)) = (у - 16)/(4 - 16),
(х - 14)/(-12) = (у - 16)/(-12),
х - 14 = у - 16
х - у + 2 = 0
у = х + 2.
б) Высота из точки С на АВ - перпендикуляр СН.
Составляем уравнение стороны АВ:
АВ: (х - 2)/(14-2) = (у - 24)/(16-24),
(х - 2)/12 = (у - 24)/(-8), сократим знаменатели на 4:
(х - 2)/3 = (у - 24)/(-2),
-2х + 4 = 3у - 72,
2х + 3у - 76 = 0,
у = (-2/3)х + (76/3).
Угловой коэффициент высоты СН, перпендикулярной к стороне АВ равен:
к(СН) = -1/(к(АВ) = -1/(-2/3) = 3/2.
Уравнение имеет вид у = (3/2)х + в.
Для определения в подставим координаты точки С.
-16 = (3/2)*2 + в,
в = -16 - 3 = -19.
Получаем уравнение СН: у = (3/2)х - 19.
Координаты точки пересечения высоты СН и медианы ВМ находим, приравнивая уравнения этих прямых.
(3/2)х - 19 = х + 2,
(1/2)х = 21, отсюда находим х = 21*2 = 42, у = 42 + 2 = 44.
ответ: точка пересечения СН и ВМ (42; 44).
ответ: Кажется так.
Объяснение:
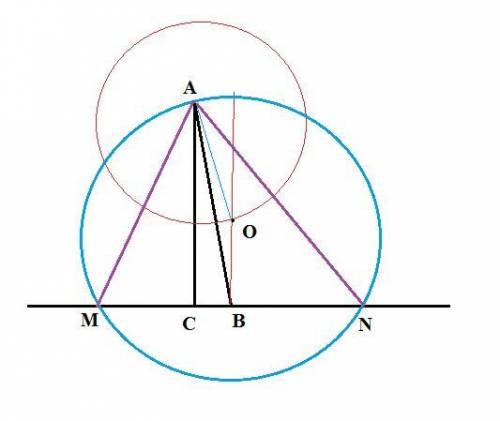
1. Строим прямоугольный треугольник по катету АС (высота) и гипотенузе АВ (медиана).
2. Прямая, содержащая катет ВС содержит и сторону искомого треугольника, лежащую против вершины этого же треугольника А.
3. Центр описанной окружности лежит на пересечении серединных перпендикуляров. Построим серединный перпендикуляр через тоску В к противолежащей вершине А стороне.
4. Из вершины А проведем дугу до пересечения с серединным перпендикуляром в точке О с заданным радиусом. Точка О будет центром описанной окружности.
5. Построив окружность, в точках пересечения окружности с прямой ВС, то есть в точках M и N получим еще две вершины искомого треугольника. АМN и есть искомый треугольник.
Для тупоугольного треугольника центр окружности будет лежать вне треугольника.
Для прямоугольного медиана будет равна радиусу окружности, один катет равен высоте, а угол А = 90 градусов..
B = 180 - 55 = 125
D = 180 - 159 = 21