АВ перпендикулярна плоскости альфа
АС, АВ - наклонная
Угол АСВ=30°
Угол АДВ=60°
Радиус окружности=√3
Найти: АВ
Т.к. АВ перпендикулярна плоскости альфа, то В проекция точки А на плоскости альфа, ВС и ВД - проекция АС и АД
На плоскости альфа, соответственно ВС принадлежит плоскости альфа
ВД принадлежит плоскости альфа, т.к. АВ перпендикулярна плоскости альфа,то ВС перпендикулярна плоскости альфа, ВД перпендикулярна плоскости альфа, значит АВ перпендикулярна ВС, АВ перпендикулярна ВД, и треугольники АВС и АВД - прямоугольные
Треугольник АВС:АВ/АС=sin угла АСВ
АС=АВ/sin угла АСВ=АВ/sin30°=АВ/1/2=2АВ
Треугольник АВД=АВ/АД=sin угла АДВ
АД=АВ/sin угла АДВ=АВ sin60°=AB/√3/2=2/√3AB
Треугольник АСД - прямоугольный (угол АСВ+угол АДВ=90°)
Значит: R=1/2СД, тогда CД=2*√3=2√3
По теореме Пифагора:
Треугольник АСД=АС²+АД²=СД²
2АВ²+2/√3АВ²=2√3²
4АВ²+4/3АВ²=12
16/3АВ²=12 |:3/16
АВ²=9/4
АВ=3/2
ответ: АВ=3/2
Объяснение:
1) CB = AB = 8, AC = 8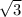 , <A = <C = 30 <B = 120
, <A = <C = 30 <B = 120
2) 400 * sin113 * sin53 / sin14
3) AC = 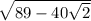
<A = Arccos( (AC^2 + AB^2 -BC^2)/2AC*AB )
<B = Arccos( (BC^2 + AB^2 -AC^2)/2BC*AB )
Если нужно найти приближенное целочисленное значение нужно подставить и посчитать на калькуляторе
Объяснение:
1) <C = 180-120-30 = 30 значит треугольник ABC равнобедренный с основанием AC. CB = AB = 8. Пусть BD высота, она же медиана.
<DBA = 120 / 2 = 60. AD = AB * sin<DBA = 8* 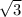 /2 = 4
/2 = 4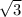
AC = 2AD = 8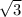
2) BC = AC * sinA / sinB
S = AC * BC * sinC / 2 = 20* 20 * sin113 * sin53 / sin14
3) AC = 
так как все стороный найдены можно подставить их значения в формулы:
<A = Arccos( (AC^2 + AB^2 -BC^2)/2AC*AB )
<B = Arccos( (BC^2 + AB^2 -AC^2)/2BC*AB )
Если нужно найти приближенное целочисленное значение нужно подставить и посчитать на калькуляторе
Відповідь:
сума основ данної трапеції=8 см
Пояснення:
1)Вписати коло в трапецію можна тільки за одної умови: тільки тоді , коли сума основ буде дорівнювати сумі бокових сторін!
Маємо АВСД-трапеція. ВС і АД-основи , АВ і СД бокові сторони.
ВС+АД+АВ+СД=16 де 16 це величина периметра трапеції.
(ВС+АД) сума основ ,( АВ+СД) сума бокових сторін
згідно 1 пункту, ВС+АД=АВ+СД беремо замість АВ+СД ВС+АД
і маємо: 2 (ВС+АД)=16 ВС+АД=16/2=8 задача розвязана.