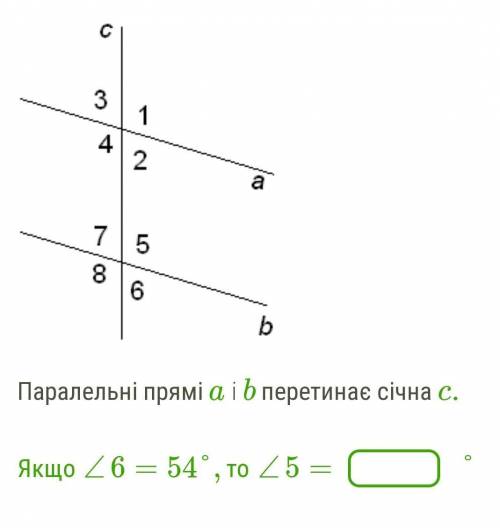
Объяснение:
a║b, c - секущая.
∠6 = 54°.
Найти: ∠5.
∠5 и ∠6 - смежные.
Сумма смежных углов равна 180°:
∠5 + ∠6 = 180°
⇒ ∠5 = 180° - ∠6 = 180° - 54° = 126°.
14; 30, 30, 120
Объяснение:
угол SRP=180-120=60
угол SPR=90-60=30 (по первому свойству прямоугольного треугольника)
угол RPQ=180-120):2=30( т.к. треугольник RPQ равнобедренный)
угол SPQ=30+30=60
угол SQP=90-60=30 (по первому признаку прямоугольного треугольника)
PQ=7*2=14 (по второму признаку прямоугольного треугольника)
угол А=30, т.к. CD= 1/2АС (по третьему признаку прямоугольного треугольника)
угол В=30, т.к. треугольник АВС равнобедренный (по свойству равнобедренного треугольника)
угол АСВ=180-30*2=120
1) Раз ВО разделила угол В пополам, то угол ОВС=1/2 углаВ=160/2=80о. Отношение 3:5 показывает, что угол В разделен на 8 частей и 3 части, т. е. 160/8*3=60о приходится на угол АВЕ, а 160/2*5=100о приходится на угол ЕВС. Отсюда угол ЕВО= разности между углами ЕВС и ОВС, т. е. 100о-80о=20о. Получается, что на чертеже луч ВЕ расположен правее луча ВО.
2) Обозначим высоту ВН.
Р тр-ка АВН: АВ+АН+5=18;
Р тр-ка НВ: ВС+НС+5=26. Сложим эти равенства:
АВ+АН+ВС+НС+10=44; АВ+ВС+(АН+НС) =34; АВ+ВС+АС=34, а левая часть это и есть периметр тр-ка АВС.
3) Взят острый угол между высотами 20о. Значит смежный с ним будет 160о. Теперь мы можем определить угол при вершине: 360о-160о-2*90о=20о. (Сумма внутренних углов в выпуклом четырехугольнике равна 360о. ) Тогда на долю двух углов при основании приходится 180о-20о=160о, а на долю каждого по 80о, т. к. углы при основании в равнобедренном тр-ке равны.
/5=126
Объяснение:
/6 =/7
/5=/8
/8+/6=180 градус
/8+54=180
/8=180-54
/8=126 градус
/8=/5 и так /5=126