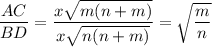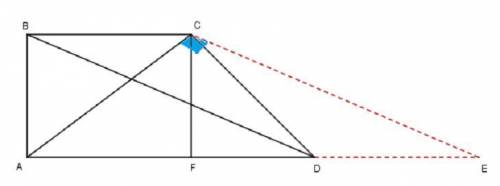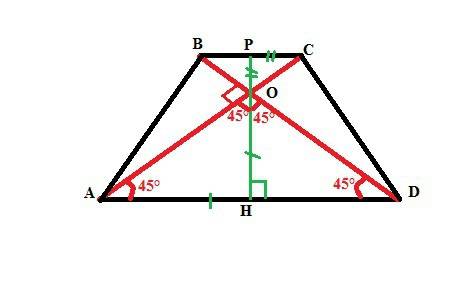
В прямоугольной трапеции ABCD с основаниями BC и AD и высотой AB диагонали AC и BD перпендикулярны друг другу . Известно отношение оснований BC : AD = m : n . Найдите отношение длин диагоналей AC : BD.
Пусть BC = mx и AD = nx. Из вершины С проведём прямую параллельной диагонали BD до пересечения прямой на продолжении основания AD, AC ⊥ CE.

Из вершины угла С проведем высоту CF.
Из прямоугольного треугольника ACE, каждый катет есть среднее пропорциональное между проекцией катета и гипотенузой:
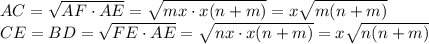
Следовательно,